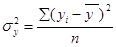Использование способов парной корреляции для изучения стохастических зависимостей
Одной из основных задач корреляционного анализа является определение влияния факторов на величину результативного показателя (в абсолютном измерении). Для решения этой задачи подбирается соответствующий тип математического уравнения, которое наилучшим образом отражает характер изучаемой связи (прямолинейной, криволинейной и т.д.). Это играет важную роль в корреляционном анализе, потому что от правильного выбора уравнения регрессии зависят ход решения задачи и результаты расчетов. Обоснование уравнения связи делается с помощью сопоставления параллельных рядов, группировки данных и линейных графиков. Размещение точек на графике покажет, какая зависимость образовалась между изучаемыми показателями — прямолинейная или криволинейная. Наиболее простым уравнением, которое характеризует прямолинейную зависимость между двумя показателями, является уравнение прямой Ух = а + Ьх, (6.1) где х — факторный показатель; У— результативный показатель; а и Ь — параметры уравнения регрессии, которые требуется отыскать. Это уравнение описывает такую связь между двумя признаками, при которой с изменением на определенную величину факторного показателя наблюдается равномерное возрастание или убывание значений результативного показателя. Для иллюстрации корреляционного анализа прямолинейной зависимости могут быть использованы сведения об изменении урожайности зерновых культур (У) в зависимости от качества пахотной земли (х) (см. табл. 4.8). Значения коэффициентов я и /> находят из системы уравнений, полученных по способу наименьших квадратов. В данном случае система уравнений имеет следующий вид:
где п — количество наблюдений (в нашем примере — 20). Значения ∑x, ∑y, ∑x2, ∑xy рассчитывают на основании фактических исходных данных (табл. 6.1).
124 125 V:.-.'
Расчет производных величин для определения параметров уравнения связи и коэффициента корреляции
Подставим полученные значения в систему уравнений:
Отнимем от второго уравнения первое. Отсюда 1000b = 400; b = 0,4;
В итоге уравнение связи, которое описывает зависимость урожайности от качества почвы, будет иметь следующий вид: Yx = 7.0 + 0.4x. Коэффициент а — постоянная величина результативного показателя, которая не связана с изменением данного фактора. Параметр b показывает среднее изменение результативного показателя с повышением или понижением величины факторного показателя на единицу его измерения. В данном примере с увеличением качества почвы на один балл урожайность зерновых культур повышается в среднем на 0,4 ц/га. Подставив в уравнение регрессии соответствующие значения х, можно определить выравненные (теоретические) значения результативного показателя (Y) для каждого предприятия. Например, для первого предприятия, где качество почвы оценивается 32 баллами, урожайность зерновых культур составит Ух = 7 + 0,4 -32 = 19,8 ц/га. Полученная величина показывает, какой была бы урожайность при качестве почвы 32 балла, если бы данное предприятие использовало свои производственные возможности в такой степени, как в среднем все предприятия района. Аналогичные расчеты сделаны для каждого наблюдения. Данные приведены в последней графе табл. 6.1. Сравнение фактического уровня урожайности с расчетным позволяет оценить результаты работы отдельных предприятий. По такому же принципу решается уравнение связи при криволинейной зависимости между изучаемыми явлениями. Если при увеличении одного показателя значения другого возрастают до определенного уровня, а потом начинают снижаться (например, зависимость производительности труда рабочих от их возраста), то для записи такой зависимости лучше всего подходит парабола второго порядка Yx = а + Ьх + сх2. (6.2) В соответствии с требованиями метода наименьших квадратов для определения параметров a, b и с необходимо решить следующую систему уравнений:
. Значения ∑x, ∑y, ∑xy, ∑x2,∑x3, ∑x4 находят на основании исходных данных (табл. 6.2). Подставив полученные значения в систему уравнений, получим
Параметры а, 6 и с находят способом определителей или способом исключения. Используем способ определителей. Сначала найдем общий определитель:
127
затем найдем частные оределители
Отсюда
Уравнение параболы получило следующее выражение: Ух= -2,67 + 4,424х- 0,561x-2. Параметры полученного уравнения экономического смысла не имеют. Если подставить в данное уравнение соответствующие значения л;, то получим выравненные значения производительности труда в зависимости от возраста рабочих. Результаты приведены в последней графе табл. 6.2. Таблица 6.2 Зависимость производительности труда (Y) от возраста работников (Л)
Из таблицы видно, что производительность труда рабочих повышается до 40-летнего возраста, после чего начинает снижаться. Значит, те предприятия, которые имеют больше работников 30—40-лет- него возраста, будут иметь и более высокие показатели производительности труда при прочих равных условиях. Этот фактор необходимо учитывать при планировании уровня производительности труда и при подсчете резервов ее роста. Довольно часто в экономическом анализе для записи криволинейных зависимостей используется гипербола
Для определения ее параметров необходимо решить следующую систему уравнений:
Гипербола описывает такую зависимость между двумя показателями, когда при увеличении одной переменной значения другой увеличиваются до определенного уровня, а потом прирост снижается, например зависимость урожайности от количества внесенного удобрения, продуктивности животных от уровня их кормления, себестоимости продукции от объема производства и т.д. При более сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвертого порядка и т.д.), а также квадратические, степенные, показательные и другие функции. Таким образом, используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, т.е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу. Однако регрессионный анализ не дает ответа на вопрос, тесная это связь или нет, решающее воздействие оказывает данный фактор на величину результативного показателя или второстепенное. Для измерения тесноты связи между факторными и результативными показателями исчисляется коэффициент корреляции. В случае прямолинейной формы связи между изучаемыми показателями он рассчитывается по следующей формуле:
128 129
Подставив значения ∑xy,∑x,∑x2,∑y,∑y2 в формулу из табл. 6.1, получим его значение, равное 0,66:
Коэффициент корреляции может принимать значения от 0 до 1. Чем ближе его величина к единице, тем более тесная связь между изучаемыми явлениями, и наоборот. В данном случае величина коэффициента корреляции является существенной (/- = 0,66). Это позволяет сделать вывод о том, что качество почвы — один из основных факторов, от которых в данном районе зависит уровень урожайности зерновых культур. Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации (d — 0,435). Он показывает, что урожайность зерновых культур на 43,5% зависит от качества почвы, а на долю других факторов приходится 56,5% ее прироста. Что касается измерения тесноты связи при криволинейной форме зависимости, то здесь используется не линейный коэффициент корреляции, а корреляционное отношение, формула которого имеет следующий вид:
Формула (6.6) является универсальной. Ее можно применять для исчисления коэффициента корреляции при любой форме зависимости. Однако при этом вначале необходимо решить уравнение регрессии и рассчитать выравненные значения результативного показателя (Ух) для каждого наблюдения, а также квадраты отклонений фактических значений 7 от его среднего и выравненного уровней (табл. 6.3).
Таблица 6.3 Расчет исходных данных для определения корреляционного отношения при криволинейной зависимости
Подставив полученные значения в формулу (6.6), определим величину корреляционного отношения, характеризующего тесноту связи между производительностью труда и возрастом рабочих:
В заключение необходимо отметить, что мы рассмотрели использование способов парной корреляции только на двух примерах. Однако эта методика может быть использована для исследования соотношений между разными экономическими показателями, что позволяет значительно углубить знания об изучаемых явлениях, оценить место и роль каждого фактора в изменении уровня исследуемого показателя.
|

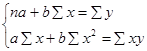
 Таблица 6.1
Таблица 6.1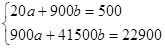

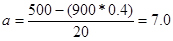



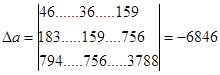







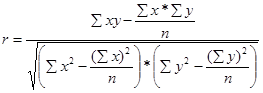
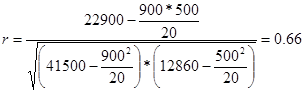
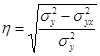 где
где