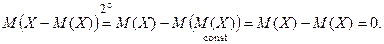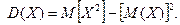Формула Муавра – Лапласа
Параметр устанавливает размер пакета данных при чтении из оперативной памяти. Возможные значения — 4, 8. Они определяют длину пакета данных. При 8 теоретически должна обеспечиваться большая производительность памяти, но на практике разница может оказаться почти незаметной.
Формула Муавра – Лапласа n достаточно велико (n ≥ 10) n ≠ 0; p ≠ 1.
Формула Пуассона n достаточно велико; p – мало.
Интегральная теорема Лапласа
Функция Лапласа вводится
причем Φ(– x) = Φ(x), x > 5, можно считать, что Φ(x) = 0,5.
Тогда
Свойства математического ожидания M (X) 1) M (C) = C 2) Если случайные величины X, Y независимы, то M (X + Y) = M (X) + M (Y) 3) M (XY) = M (X) M (Y). 4) M (CX) = CM (X).
Дисперсией называется математическое ожидание квадрата отклонения.
Дисперсия характеризует степень рассеивания значений случайной величины X от математического ожидания X. Свойства D (X) 1) D (C) = 0; 2) D (X + Y) = D (X) + D (Y), если X, Y независимы. 3) D(CX) = C 2 D (X) Теорема. Среднее квадратическое отклонение σ;(X)
Случайная величина X 0 называется нормированной, если её математическое ожидание равно нулю, а дисперсия равна 1.
Законы распределения дискретной случайной величины 1) биноминальный Х – число появлений события А в n испытаниях, p – вероятность появления А в каждом испытании.
Теорема. Если дискретная случайная величина X распределена по бинональному закону с параметром p, то математическое ожидание M (X) = np. Теорема. Если дискретная случайная величина X распределена по бинональному закону с параметром p, то D (X) = npq. Закон Пуассона X – число появлений А в n опытах n – велико p – вероятность А в каждом опыте p – мало
Теорема. Если дискретная случайная величина распределена по закону Пуассона с параметром λ;, то M(X) = λ; D (X) = λ;.
|



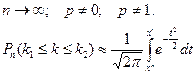







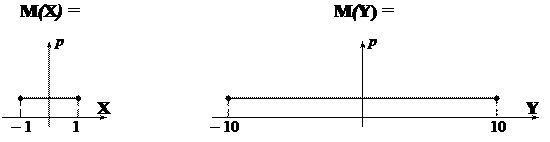 X – M (X) – отклонение X.
X – M (X) – отклонение X.