Задания для самостоятельного решения. 1. Даны матрицы , , . Существуют ли а)
1. Даны матрицы в) 2. Найдите б) 3. Даны матрицы: Найдите а) д) 4. Даны матрицы: Найдите а) ж)
5. Найти: a) 3A+2B, если б) д) ж) к) 6. Найти значение многочлена а) б) в) 7. Найти матрицы, обратные для данных и сделать проверку: а) 8. Найти ранг матрицы: а) г) Ответы: 1. а), в), е), ж) да; б), г), д), з) нет. 2. а) 3;5, б) 3;6, в) 3. а) в) ж) 4. а) д) 5. а) 6. а) 7. а) г) 8. а)2; б)3; в)3; г)2; д)1; е)2. Системы линейных уравнений Основные понятия Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида:
где числа Матрица, составленная из коэффициентов системы, называется основной матрицей и обозначается:
Расширенной матрицей системы называется матрица
Решение системы (1.16) называется n значений неизвестных
Определение. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Определение. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Две системы называются эквивалентными (равносильными), если каждое решение одной из них является решением другой, и наоборот. Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы. Система линейных уравнений (1.16) называется однородной, если все свободные члены равны нулю.
Однородная система всегда совместна, так как
|

 ,
,  ,
,  . Существуют ли а)
. Существуют ли а)  , б)
, б)  ,
, , г)
, г)  , д)
, д)  , е)
, е)  , ж)
, ж)  , з)
, з)  ?
? и
и 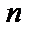 , если известно, что а)
, если известно, что а)  ;
; ; в)
; в)  .
. ,
,  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
; ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
. ,
,  ,
,  .
. ; д)
; д)  ; е)
; е)  ;
; ; з)
; з)  ; и)
; и) 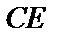 ; к)
; к)  .
.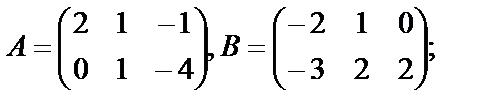
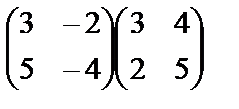 ; в)
; в)  ; г)
; г) 
 ; е)
; е)  ;
; з)
з)  и)
и)  ;
; .
. , если:
, если: , где
, где  ;
; , где
, где  ;
; , где
, где  .
. ; б)
; б) 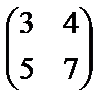 ; в)
; в)  ; г)
; г)  .
. ; б)
; б)  ; в)
; в) 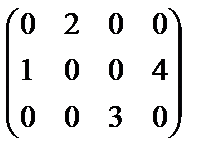 ;
; ; д)
; д)  ; е)
; е)  .
. — любые натуральные числа.
— любые натуральные числа. , б)
, б)  ,
, , г)
, г)  , д)
, д)  , е)
, е)  ,
, , з)
, з)  .
. , б)
, б)  , в)
, в) 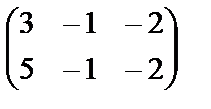 , г)
, г)  ,
, , е)
, е)  , ж) E, з)
, ж) E, з)  , и) C, к) A.
, и) C, к) A. ; б)
; б)  ; в)
; в) 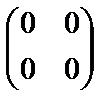 ; г)
; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  ; и)
; и)  ; к)
; к) 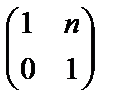 .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  ;
;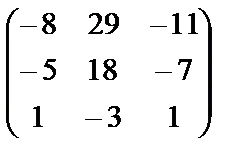 .
. (1.16)
(1.16) называются коэффициентами системы, числа
называются коэффициентами системы, числа  - свободными членами.
- свободными членами. . (1.17)
. (1.17) , полученная из основной матрицы
, полученная из основной матрицы  , дополненная столбцом свободных членов:
, дополненная столбцом свободных членов: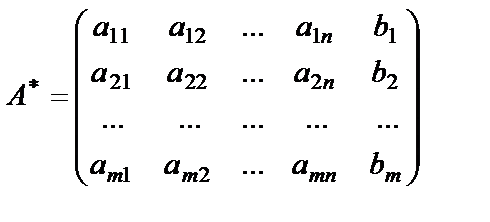 . (1.18)
. (1.18) , при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца
, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .
. (1.19)
(1.19) является решением системы. Это решение называется нулевым или тривиальным.
является решением системы. Это решение называется нулевым или тривиальным.


