Методы их вычисления
Определение. Выражение
называется определителем четвертого порядка. Этот определитель можно записать в виде:
где Формулу (6) можно записать с помощью значка суммирования
где i=1,2,3,4. Формула (7) называется разложением определителя по элементам i-ой строки. Можно записать и разложение определителя по элементам j-го столбца:
где j=1,2,3,4. Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов строки или столбца определителя в нуль с помощью свойств определителей. Пример 11. Вычислить определитель
Решение. Прибавим элементы первой строки к элементам второй строки:
Элементы первой строки умножим на (-2) и прибавим к элементам третьей строки:
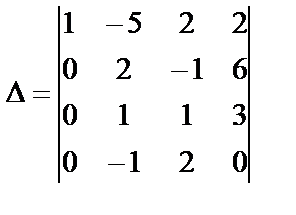
Элементы первой строки умножим на (-1) и прибавим к элементам четвертой строки:
Разложим полученный определитель по элементам первого столбца
Переставим первые две строки, при этом знак определителя изменится на противоположный, одновременно вынесем общий множитель 3 элементов третьего столбца за знак определителя:
Умножим элементы первой строки на (-2) и прибавим к элементам второй строки:
Полученный определитель разложим по элементам второй строки
Пример 12. Вычислить определитель Решение. Поменяем местами первую и вторую строки, при этом по свойству 2 знак определителя изменится на противоположный:
Сначала элементы первой строки умножим на (-2) и прибавим к элементам второй и четвертой строк, а затем элементы первой строки умножим на (-3) и прибавим к элементам третьей строки, получим:
Элементы второй строки прибавим к элементам четвертой строки:
Элементы третьей строки умножим на (-1) и прибавим к элементам четвертой строки:
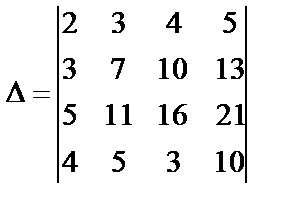
Получим определитель треугольного вида, значение которого равно произведению элементов главной диагонали Пример 13. Вычислить определитель
Решение. Разложим определитель по элементам третьей строки
Полученные определители третьего порядка вычислим по правилу треугольника
|


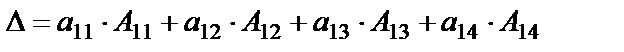 , (6)
, (6)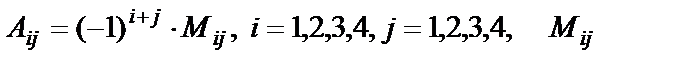 - минор элемента, стоящего на пересечении i-ой строки и j-го столбца,
- минор элемента, стоящего на пересечении i-ой строки и j-го столбца, 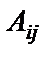 -алгебраическое дополнение этого элемента.
-алгебраическое дополнение этого элемента.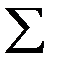 :
: , (7)
, (7) (8)
(8)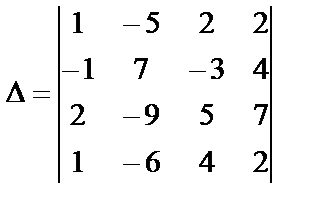 .
. .
. .
. .
.
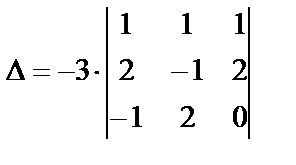 .
. .
.
 .
.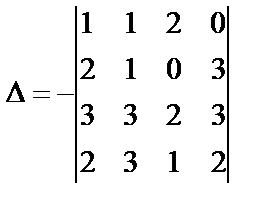 .
. .
. .
.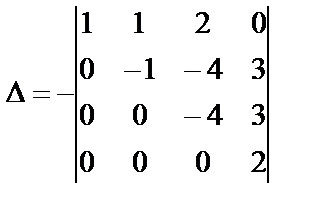 .
.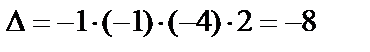 .
. .
.




