Теорема Кронекера-Капелли
Система линейных алгебраических уравнений (1.16) совместна тогда и только тогда, когда ранг расширенной матрицы (1.18) равен рангу основной матрицы (1.17), то есть Если система (1.16) совместна и 1) ранг системы равен числу неизвестных (r(A)=n), то система имеет единственное решение; 2) ранг системы меньше числа неизвестных (r(A)<n), то система имеет бесчисленное множество решений. Рассмотрим второй случай. Пусть r(A)=r<n. Возьмем первые r уравнений системы (1.16) и оставим в левых частях этих уравнений первые r неизвестных, а остальные неизвестные перенесем вправо:
“Свободным” неизвестным Пример 31. Исследовать на совместность систему
Решение. Определим ранги основной матрицы системы и расширенной матрицы системы. Для этого выпишем расширенную матрицу системы
Вертикальной чертой отделим элементы основной матрицы от свободных членов системы. Умножим элементы первой строки на (-2) и прибавим к элементам второй строки
Элементы первой строки, умноженные на (-3), прибавим к элементам третьей строки
Умножим элементы второй строки на (-2) и прибавим к элементам третьей строки
Основная матрица системы А эквивалентна матрице
В полученной матрице одна ненулевая строка, значит ранг матрицы В полученной матрице две ненулевые строки, поэтому Так как Пример 32. Исследовать на совместность систему
Решение. Выпишем расширенную матрицу системы
Поменяем местами первую и вторую строки
Умножим элементы первой строки на (-3) и прибавим к элементам второй строки
Элементы первой строки, умноженные на (-7), (-5), (-3) прибавим соответственно к элементам третьей, четвертой и пятой строк:
Поменяем местами строки
Умножим элементы второй строки на
Элементы второй строки умножим на 7, 19, 13 и прибавим соответственно к элементам третьей, четвертой и пятой строк:
Основная матрица системы эквивалентна матрице
в которой две ненулевые строки, поэтому r(A)=2. Расширенная матрица системы эквивалентна матрице
в которой также две ненулевые строки, поэтому Так как Найдем единственное решение данной системы. Для этого восстановим систему по последней матрице
Из второго уравнения найдем Пример 33. Исследовать систему уравнений
Решение. Определим ранг основной матрицы системы и ранг расширенной матрицы данной системы. Выпишем расширенную матрицу
Умножим элементы первой строки на (-1) и прибавим сначала к элементам второй строки, а затем к элементам третьей строки. В результате получим матрицу, эквивалентную матрице
Элементы второй строки умножим на
Элементы второй строки умножим на (-1) и прибавим к элементам третьей строки
Отбросим третью строку, все элементы которой равны нулю
В результате элементарных преобразований получили две ненулевые строки. Ранг основной матрицы системы равен двум r(A)=2. Ранг расширенной матрицы системы тоже равен двум Значит, данная система уравнений совместна, а так как число неизвестных, равное трем, больше, чем ранг, то система уравнений является неопределенной. Найдем общее решение системы уравнений. Воспользуемся матрицей (1.20) для получения системы уравнений, равносильной данной системе
За базисные неизвестные примем
Выразим из этой системы
Пусть
Если необходимо найти какое-либо частное решение системы, то константе С придают любое значение, например: пусть С =1, тогда получим
|

 .
.
 можно придать любые значения. Тогда соответствующие значения получают неизвестные
можно придать любые значения. Тогда соответствующие значения получают неизвестные  . Таким образом можно найти частные и общее решения исходной системы уравнений.
. Таким образом можно найти частные и общее решения исходной системы уравнений.

 ~
~  .
. .
. .
.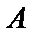 ~
~  .
. равен 1, то есть r(A)=1. Расширенная матрица системы
равен 1, то есть r(A)=1. Расширенная матрица системы  .
.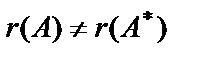 , тогда согласно теореме Кронекера-Капелли данная система уравнений несовместна.
, тогда согласно теореме Кронекера-Капелли данная система уравнений несовместна.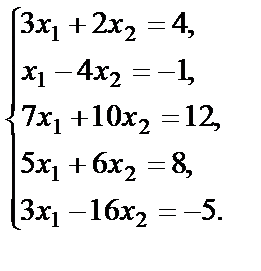








 ~
~ 
 ,
, .
. , система совместна. В данной системе уравнений две неизвестные, то есть
, система совместна. В данной системе уравнений две неизвестные, то есть 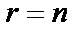 , поэтому система уравнений является определенной.
, поэтому система уравнений является определенной.
 и полученное значение подставим в первое уравнение
и полученное значение подставим в первое уравнение 



 .
.
 , а элементы третьей строки на
, а элементы третьей строки на 


 (1.20)
(1.20)
 и
и  , а
, а  - свободная переменная.
- свободная переменная.


 , где С – любое действительное число, получаем общее решение данной системы уравнений
, где С – любое действительное число, получаем общее решение данной системы уравнений
 .
.


