Обратная матрица
Пусть А -квадратная матрица n- го порядка
Определение. Матрица
составленная из алгебраических дополнений к элементам матрицы А, называется присоединенной к матрице А. Алгебраические дополнения к элементам квадратной матрицы находятся так же, как к элементам ее определителя. В присоединенной матрице алгебраические дополнения элементов строки стоят в столбце с таким же номером. Пример 23. Дана матрица
Найти матрицу, присоединенную к матрице А. Решение. Найдем алгебраические дополнения к элементам матрицы А:
Составим матрицу
Определение. Матрица
где Теорема. Для того, чтобы матрица Обратная матрица находится по формуле:
для матрицы А третьего порядка. Свойства обратной матрицы: 1. 2. 3. Пример 24. Найти Решение. Проверим, является ли данная матрица невырожденной. Вычислим определитель, соответствующий матрице
Найдем алгебраические дополнения элементов матрицы
Составим матрицу
Проверка:
Пример 25. Показать, что матрица
Решение. Найдем произведение матриц
Следовательно, матрица Пример 26. Найти матрицу, обратную для матрицы
Решение. Найдем определитель матрицы
Матрица
Пример 27. Найти матрицу, обратную для данной матрицы
Решение. Найдем определитель матрицы
значит матрица
Вычислим алгебраические дополнения элементов матрицы
Используя формулу (15), составим матрицу
Проверка:
Значит обратная матрица
|

 .
.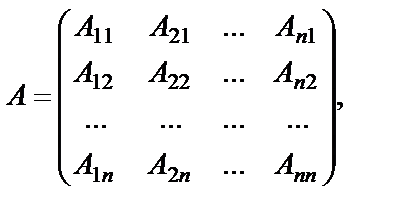










 , присоединенную к матрице А
, присоединенную к матрице А .
.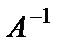 называется обратной матрице А, если выполняется условие
называется обратной матрице А, если выполняется условие , (14)
, (14) – единичная матрица того же порядка, что и матрица
– единичная матрица того же порядка, что и матрица  . Матрица
. Матрица  .
. то есть чтобы матрица была невырожденной.
то есть чтобы матрица была невырожденной. (15)
(15)



 следовательно, матрица
следовательно, матрица 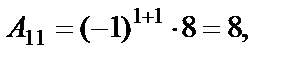




 Следовательно, обратная матрица
Следовательно, обратная матрица  , если
, если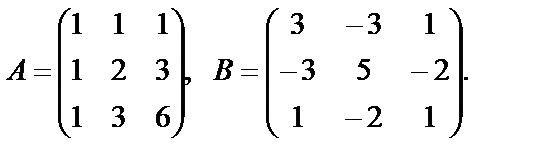
 :
:

 является обратной для матрицы
является обратной для матрицы  .
.
 :
: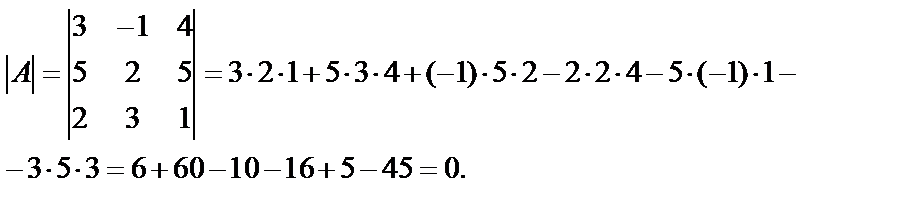







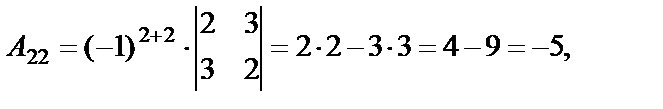
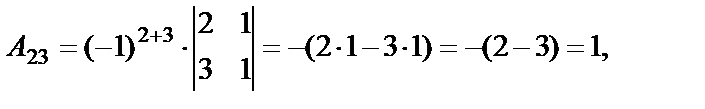



 .
.




