Ранг матрицы
Рассмотрим матрицу
Выделим в ней k строк и k столбцов Определение. Рангом матрицы Обозначают ранг матрицы Пример 28. Найти ранг матрицы:
Решение. Дана матрица размера
Составим минор второго порядка, например
Ранг матрицы удобно вычислять, используя элементарные преобразования над матрицей. К элементарным относятся следующие преобразования: 1) перестановка местами двух параллельных рядов матрицы; 2) умножение всех элементов ряда матрицы на число, отличное от нуля; 3) прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число. Определение. Две матрицы Свойства ранга матрицы: 1. При транспонировании матрицы ее ранг не меняется. 2. Ранг матрицы не изменится, если вычеркнуть из матрицы нулевой ряд. 3. При элементарных преобразованиях ранг матрицы не изменяется, т.е. если Пример 29. Найти ранг матрицы
Решение. Умножим элементы первой строки на (-2) и прибавим к элементам третьей строки
Элементы второй строки умножим на 3 и прибавим к элементам третьей строки
Вычеркнем третью строку полученной матрицы, т.к. все ее элементы равны нулю:
Составим минор второго порядка:
Таким образом, В преобразованной матрице получилось две ненулевые строки. Пример 30. Найти ранг матрицы
Решение. Умножим элементы первой строки на (-2) и прибавим к элементам второй строки данной матрицы:
Умножим элементы первой строки на (-3) и прибавим к элементам третьей строки:
Элементы второй строки полученной матрицы умножим на (-5) и прибавим к элементам третьей строки:
Из элементов полученной матрицы составим определитель третьего порядка. Для этого возьмем первые три столбца:
Получили определитель треугольного вида, значение которого равно произведению элементов главной диагонали
Ранг последней матрицы равен 3, следовательно, ранг данной матрицы тоже равен 3. В последней матрице содержится три ненулевые строки. Можно сделать следующий вывод: ранг матрицы равен количеству ненулевых строк преобразованной к треугольному виду матрицы.
|

 размера
размера 
 .
. . Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы.
. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы. или
или  .
.
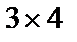 . Возможный ранг матрицы равен трем, т.к.
. Возможный ранг матрицы равен трем, т.к.  . Но матрица содержит два нулевых столбца, поэтому все определители третьего порядка, составленные из элементов данной матрицы равны нулю:
. Но матрица содержит два нулевых столбца, поэтому все определители третьего порядка, составленные из элементов данной матрицы равны нулю: ,
,  ,
,  .
. . Значит,
. Значит, 
 называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается
называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается  ~ В.
~ В.

 ~
~ 
 ~
~ 
 ~
~  .
. .
. .
. ~
~  .
. .
.
 .
. .
.


