Свойства определителей
Следующие свойства справедливы для определителей любого порядка, позволяют упростить вычисления определителей. Свойство 1. Определитель не меняет своего значения, если его строки заменить столбцами с теми же номерами, а столбцы строками, то есть
Введенное действие называется транспонированием строк и столбцов. Свойство 2. Если переставить две строки (столбца) определителя, то знак значения определителя изменится на противоположный:
Свойство 3. Если определитель имеет две одинаковых строки или два одинаковых столбца, то он равен нулю:
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно выносить за знак определителя:
Свойство 5. Если все элементы какого-либо ряда определителя равны нулю, то определитель равен нулю:
Свойство 6. Если две строки (столбца) определителя пропорциональны, то определитель равен нулю:
Свойство 7. Если элементы какого-либо ряда определителя представляют собой сумму двух слагаемых, то определитель можно представить в виде суммы двух определителей, у которых все ряды, кроме данного, прежние, а в данном ряду в первом определителе стоят первые слагаемые, а во втором определителе – вторые:
Свойство 8. Величина определителя не изменится, если к элементам какой-либо строки (столбца) определителя прибавить элементы параллельной строки (столбца), умноженные на одно и то же число:
Пример 8. Вычислить определитель
Решение. Элементы первого и второго столбцов данного определителя пропорциональны Пример 9. Вычислить определитель
Решение. Используя свойство 8, приведем данный определитель к треугольному виду. Для этого элементы первой строки умножим на (-1) и прибавим к элементам второй строки:
Элементы первой строки умножим на (-4) и прибавим к элементам третьей строки:
Элементы второй строки умножим на 2 и прибавим к элементам третьей строки:
Получили определитель треугольного вида (под главной диагональю определителя все элементы равны нулю), и поэтому значение определителя будет равно произведению элементов главной диагонали преобразованного определителя:
Пример 10. Вычислить определитель
Решение.
Воспользовались свойством 7, а так как в первом полученном определителе первые две строки одинаковые, то по свойству 3 этот определитель равен нулю, поэтому
Элементы третьей строки содержат общий множитель 2, который, согласно свойства 4, можно вынести за знак определителя:
Полученный определитель содержит две одинаковые строки вторую и третью, поэтому по свойству 3 этот определитель, а значит и данный, равен нулю:
|


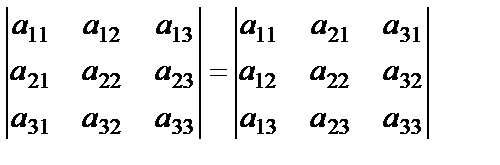 .
. .
. .
. .
. .
. .
. .
. .
. , используя свойства определителей.
, используя свойства определителей. , поэтому, согласно свойству 6, данный определитель равен нулю, то есть
, поэтому, согласно свойству 6, данный определитель равен нулю, то есть  .
. , используя свойства определителей.
, используя свойства определителей. .
. .
. .
. .
. , используя свойства определителей.
, используя свойства определителей. .
. .
. .
. .
.


