Определители третьего порядка
Определение. Определителем третьего порядка, соответствующим квадратной таблице элементов
называется число, определяемое равенством
Пример 4. Вычислить определитель
Решение. По определению получим: Если в формуле (2) раскрыть определители второго порядка и собрать слагаемые с одинаковыми знаками, то получим:
Этот способ вычисления определителя третьего порядка называется правилом треугольника.
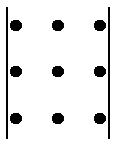
Первые три слагаемых для вычисления определителя есть сумма произведений элементов главной диагонали и элементов, расположенных в вершинах треугольников, как они показаны линиями на первом рисунке; оставшиеся слагаемые есть сумма произведений, взятых со знаком минус, элементов побочной диагонали и элементов, расположенных в вершинах треугольников, как они показаны линиями на втором рисунке. Пример 5. Вычислить определитель Решение. Перемножим элементы главной диагонали определителя Таким образом Определение. Определитель, в котором под главной диагональю (над главной диагональю) стоят нули, называется определителем треугольного вида. Определитель треугольного вида равен произведению элементов главной диагонали. Пример 6. Вычислить определитель Решение. По условию дан определитель треугольного вида, т.к. под главной диагональю этого определителя стоят нули, значит значение данного определителя равно произведению элементов главной диагонали, то есть Определение. Минором элемента определителя третьего порядка называется определитель второго порядка, полученный из данного определителя путем вычеркивания строки и столба, на пересечении которых стоит данный элемент. Минор элемента Например, для определителя
миноры Определение. Алгебраическим дополнением данного элемента определителя 3-го порядка называется минор этого элемента, умноженный на Алгебраическое дополнение элемента Для определителя третьего порядка знак, который при этом приписывается минору соответствующего определителя, определяется следующей таблицей: Из определения определителя третьего порядка следует, что
Верна общая теорема разложения: определитель третьего порядка равен сумме произведений элементов любой его строки или столбца на соответствующие этим элементам алгебраические дополнения. Таким образом, имеют место шесть разложений:
Отметим, что сумма произведений элементов какого-либо ряда (строки или столбца) на алгебраические дополнения элементов параллельного ряда равна нулю. Пример 7. Вычислить определитель разлагая его по элементам третьего столбца. Решение. Согласно теореме разложения имеем:
|

 ,
, (2)
(2) .
.
 (3)
(3)

 по правилу треугольника.
по правилу треугольника.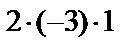 , затем – элементы, лежащие на параллелях к этой диагонали, и элементы из противоположного угла определителя согласно правилу треугольника
, затем – элементы, лежащие на параллелях к этой диагонали, и элементы из противоположного угла определителя согласно правилу треугольника  ,
,  . Элементы, входящие в формулу (3) со знаком минус, вычисляем аналогично, но относительно побочной диагонали:
. Элементы, входящие в формулу (3) со знаком минус, вычисляем аналогично, но относительно побочной диагонали:  ,
,  ,
,  .
.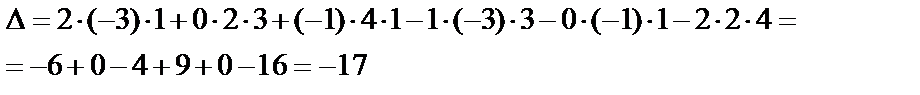
 .
. .
.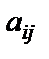 , стоящего на пересечении i -ой строки и j -го столбца определителя, обозначают
, стоящего на пересечении i -ой строки и j -го столбца определителя, обозначают  .
.
 ,
, 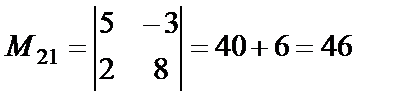 .
. , где k равно сумме номера строки и номера столбца, на пересечении которых находится этот элемент.
, где k равно сумме номера строки и номера столбца, на пересечении которых находится этот элемент.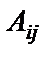 . Согласно определению
. Согласно определению  .
. .
. .
. (5)
(5) ,
,



