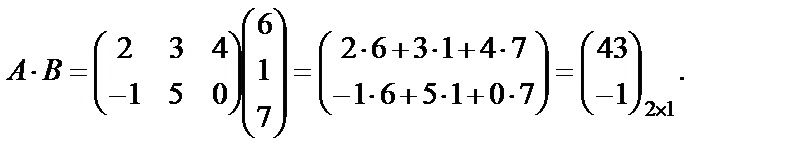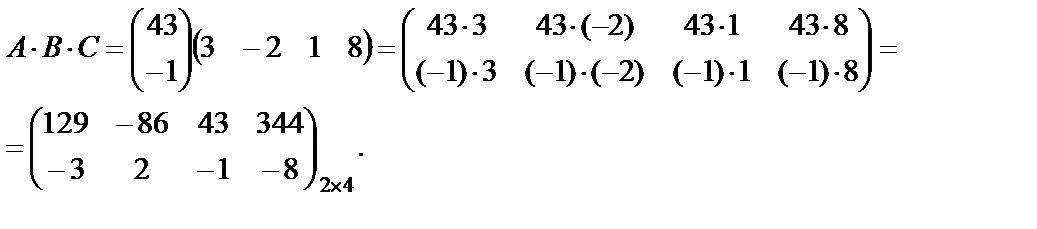Определение. Суммой двух матриц 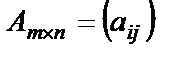 и
и 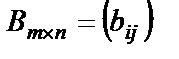 одинаковых размеров называется матрица того же размера
одинаковых размеров называется матрица того же размера 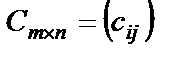 такая, что
такая, что 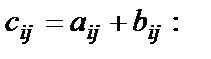
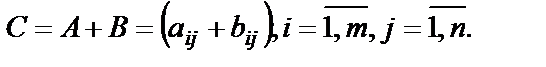 (10)
(10)
Пример 14. Найти сумму матриц  и
и  , если
, если 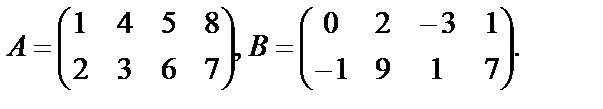
Решение. 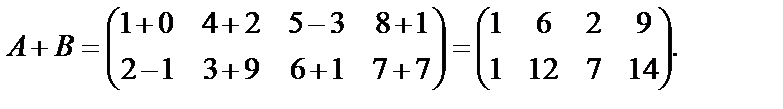
Для любых матриц 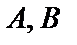 и
и 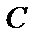 одинакового размера справедливы следующие свойства:
одинакового размера справедливы следующие свойства:
1. 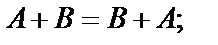
2. 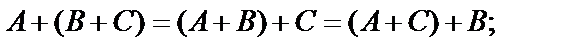
3. 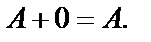 .
.
Определение. Произведением матрицы 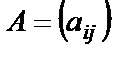 на число
на число 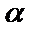 называется матрица
называется матрица 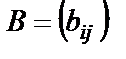 такая, что
такая, что 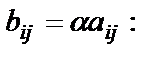
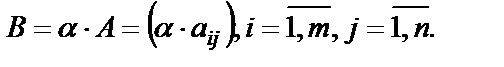 (11)
(11)
Пример 15. 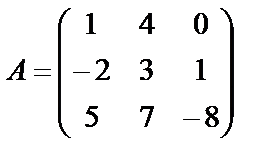 ,
, 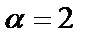 . Найти
. Найти 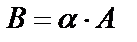 .
.
Решение. 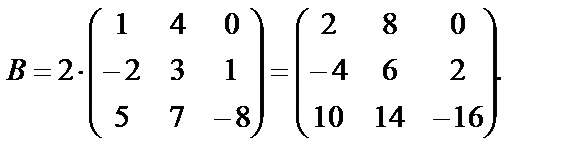
Матрица 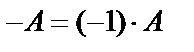 называется противоположной матрице
называется противоположной матрице  .
.
Для любых матриц  и
и  одинакового размера и любых действительных чисел
одинакового размера и любых действительных чисел 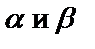 справедливы следующие свойства:
справедливы следующие свойства:
1. 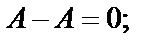
2. 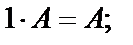
3. 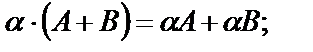
4. 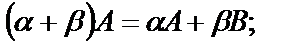
5.  .
.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Оределение. Произведением матрицы 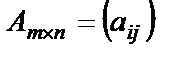 на матрицу
на матрицу 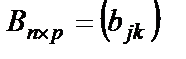 называется матрица
называется матрица 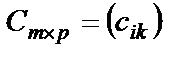 такая, что
такая, что
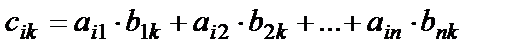 , (12)
, (12)
где 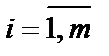 ,
, 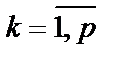 .
.
Формулу (12) для нахождения элемента 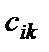 полезно помнить в виде правила:
полезно помнить в виде правила:
в матрице  выделяем
выделяем 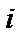 - ю строку, в матрице
- ю строку, в матрице  выделяем
выделяем 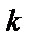 -й столбец.
-й столбец.
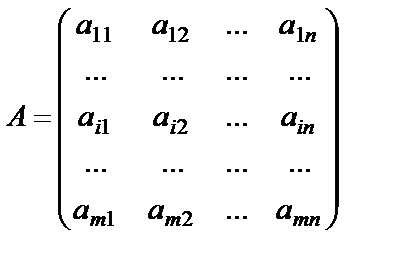 , , 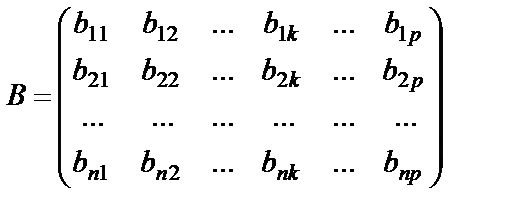 . .
|
Тогда для того, чтобы получить элемент 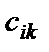 матрицы
матрицы 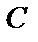 , расположенный на пересечении i-й строки и k -го столбца, надо каждый элемент i -й строки матрицы
, расположенный на пересечении i-й строки и k -го столбца, надо каждый элемент i -й строки матрицы  умножить на соответствующий элемент k -го столбца матрицы
умножить на соответствующий элемент k -го столбца матрицы  и все полученные произведения сложить.
и все полученные произведения сложить.
Если матрицы  и
и  квадратные одного размера, то произведения
квадратные одного размера, то произведения 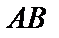 и
и 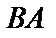 всегда существуют.
всегда существуют.
Пример 16. Найти произведение матриц  и
и  , если
, если 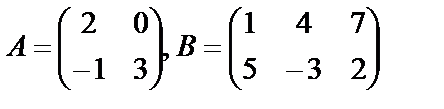 .
.
Решение. Для получения первой строки новой матрицы фиксируем в матрице  первую строку (2 0), а в матрице
первую строку (2 0), а в матрице  выделяем поочередно первый, второй и третий столбцы:
выделяем поочередно первый, второй и третий столбцы: 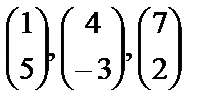 .
.
Элемент 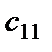 находим как сумму произведений элементов первой строки матрицы
находим как сумму произведений элементов первой строки матрицы  на соответствующие элементы первого столбца матрицы
на соответствующие элементы первого столбца матрицы  по правилу: «произведение первого элемента строки на первый элемент столбца плюс произведение второго элемента строки на второй элемент столбца».
по правилу: «произведение первого элемента строки на первый элемент столбца плюс произведение второго элемента строки на второй элемент столбца».
Пользуясь этим правилом, находим: 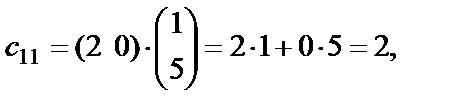
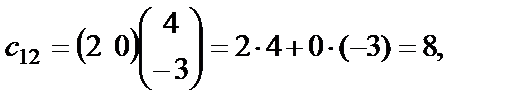
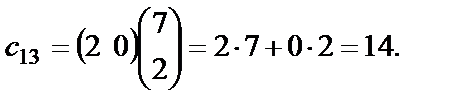
Для вычисления элементов 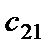 ,
, 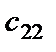 ,
, 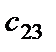 фиксируем вторую строку матрицы
фиксируем вторую строку матрицы  (-1 3) и умножаем её поочередно на первый, второй и третий столбцы матрицы
(-1 3) и умножаем её поочередно на первый, второй и третий столбцы матрицы  :
:
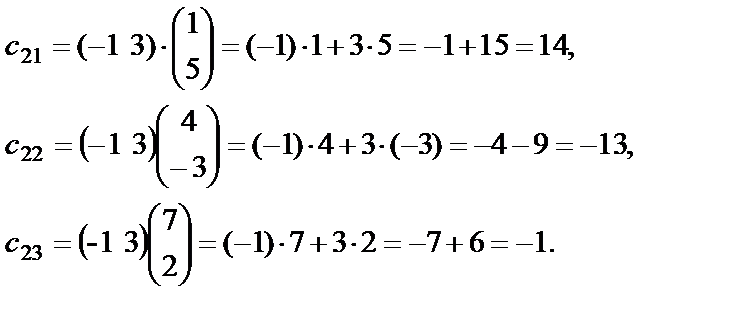
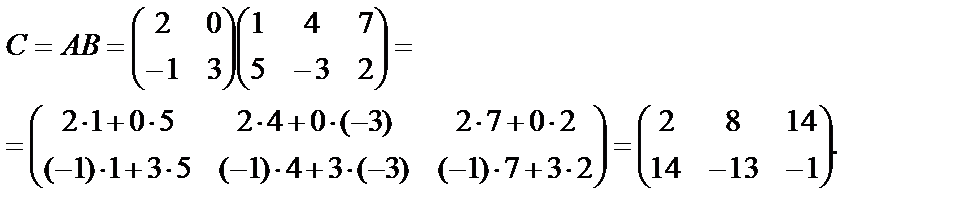
Пример 17. Даны матрицы
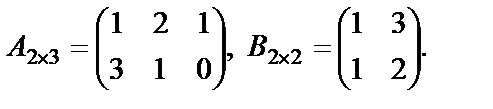 Найти
Найти 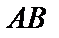 и
и 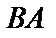 .
.
Решение. Произведение 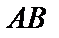 не определено, так как число столбцов матрицы
не определено, так как число столбцов матрицы  (3)не совпадает с числом строк матрицы
(3)не совпадает с числом строк матрицы  (2). Произведение
(2). Произведение 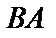 определено, так как число столбцов матрицы
определено, так как число столбцов матрицы  (2) совпадает с числом строк матрицы
(2) совпадает с числом строк матрицы  (2).
(2).
Используя правило, рассмотренное в предыдущем примере, найдем произведение 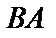 :
:
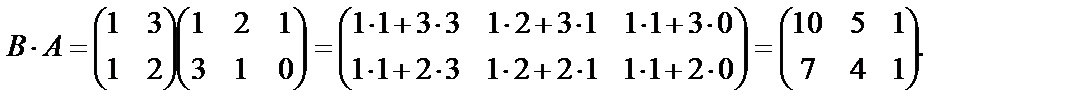 Матрицы
Матрицы  и
и  называются перестановочными, если
называются перестановочными, если 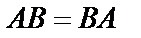 .
.
Умножение матриц обладает следующими свойствами:
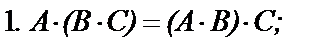
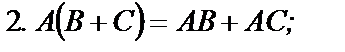
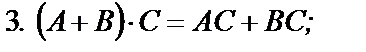
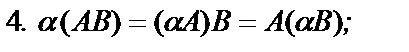
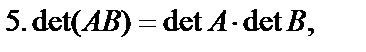 если указанные суммы и произведения матриц имеют смысл.
если указанные суммы и произведения матриц имеют смысл.
6. Если  квадратная матрица n-го порядка, Е -единичная матрица того же порядка, то
квадратная матрица n-го порядка, Е -единичная матрица того же порядка, то 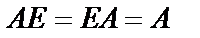 .
.
7. Для операции транспонирования верны следующие равенства:
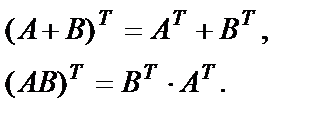
Пример 18. Даны матрицы 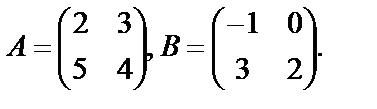
Проверить справедливость равенства 5.
Решение. Найдем произведение 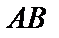 :
:
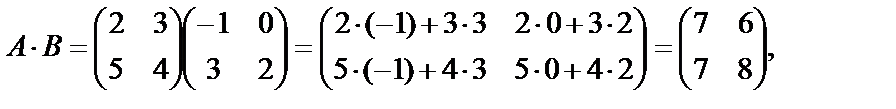
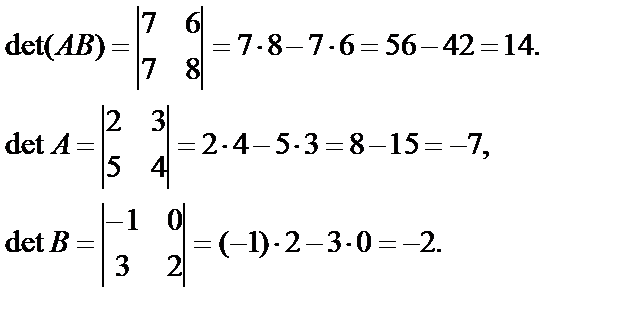
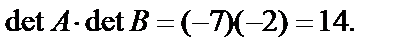
Таким образом, 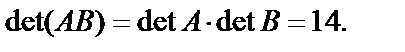
Пример 19. Даны матрицы 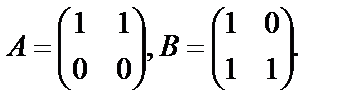
Показать, что 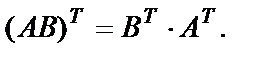
Решение. Найдем произведение матриц АВ:
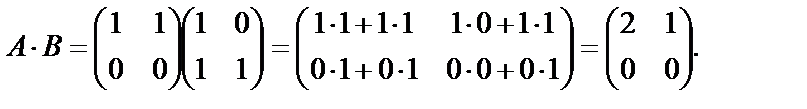
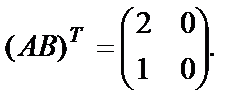

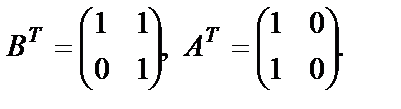
Найдем 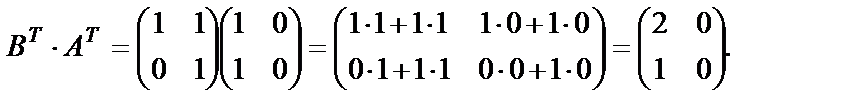
Получим 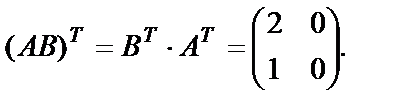
Пример 20. Даны две матрицы 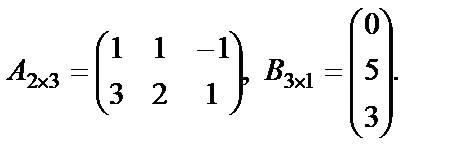
Найти АВ.
Решение.
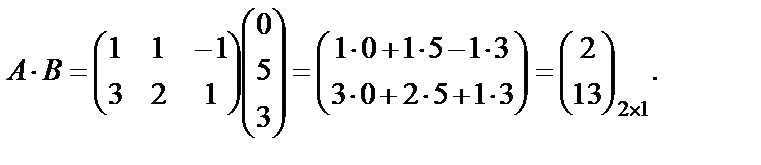
Пример 21. Найти значение матричного многочлена 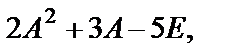 если
если 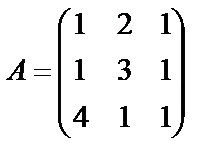 , Е - единичная матрица третьего порядка.
, Е - единичная матрица третьего порядка.
Решение. 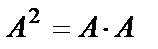 . Найдем
. Найдем 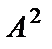 :
:
 =
= 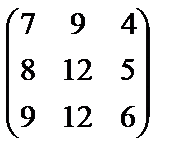 ,
, 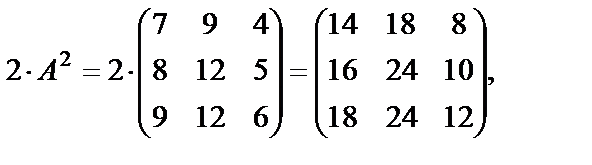
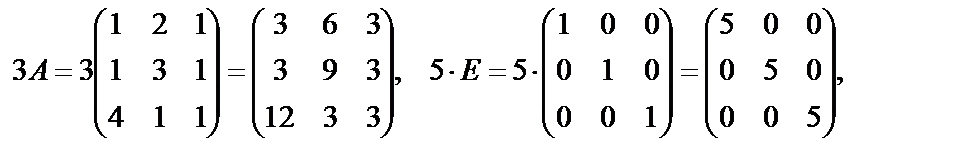
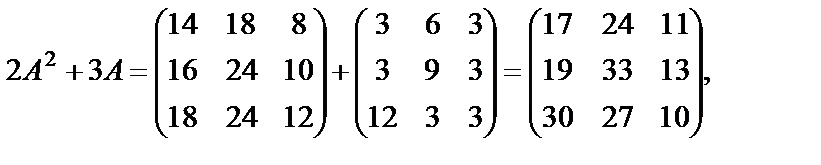
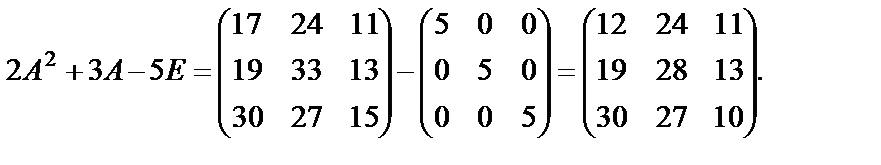
Пример 22. Найти произведение матриц 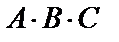 , если оно определено, где
, если оно определено, где 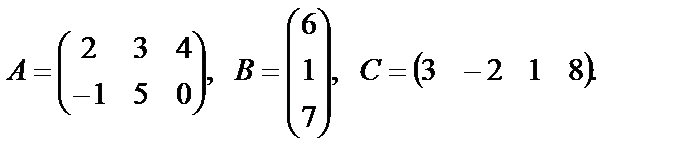
Решение. Рассмотрим матрицы  и В. Размер матрицы
и В. Размер матрицы 
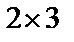 , размер матрицы
, размер матрицы 
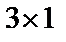 . Так как число столбцов матрицы
. Так как число столбцов матрицы  (3) равно числу строк матрицы
(3) равно числу строк матрицы 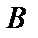 (3), то произведение
(3), то произведение 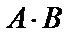 определено, в результате получим матрицу размера
определено, в результате получим матрицу размера 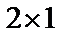 .
.
Число столбцов матрицы 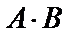 (1) совпадает с числом строк матрицы
(1) совпадает с числом строк матрицы 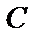 (1), таким образом, произведение
(1), таким образом, произведение 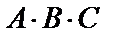 определено, получаемая матрица будет размера
определено, получаемая матрица будет размера 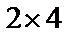 .
.
Найдем произведение 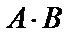 :
:
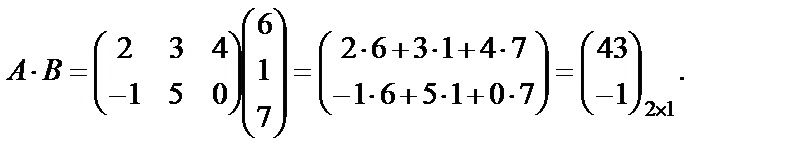
Найдем произведение 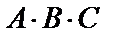 :
:
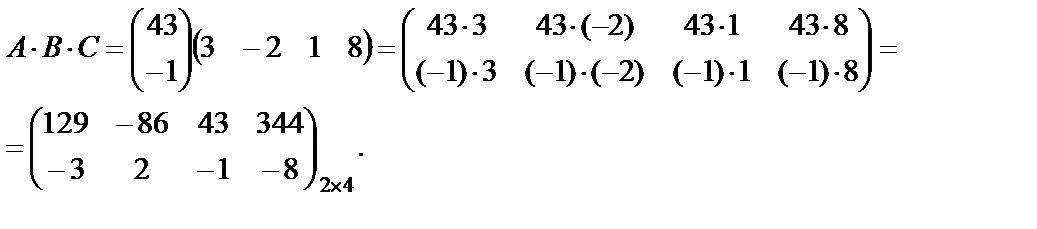

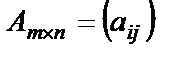 и
и 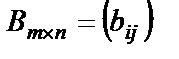 одинаковых размеров называется матрица того же размера
одинаковых размеров называется матрица того же размера 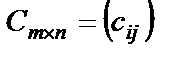 такая, что
такая, что 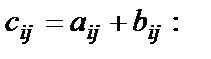
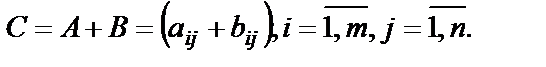 (10)
(10) и
и  , если
, если 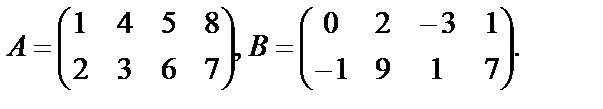
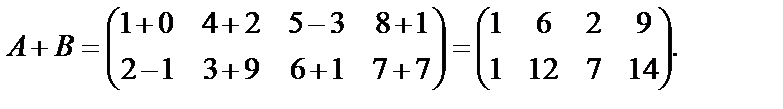
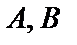 и
и 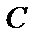 одинакового размера справедливы следующие свойства:
одинакового размера справедливы следующие свойства: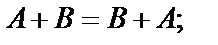
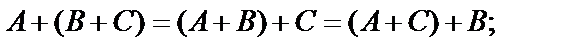
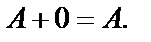 .
.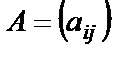 на число
на число 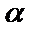 называется матрица
называется матрица 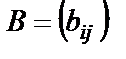 такая, что
такая, что 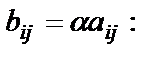
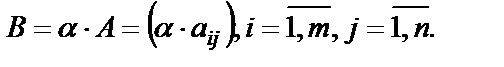 (11)
(11)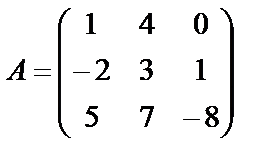 ,
, 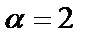 . Найти
. Найти 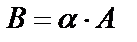 .
.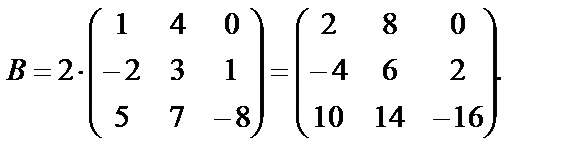
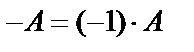 называется противоположной матрице
называется противоположной матрице 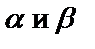 справедливы следующие свойства:
справедливы следующие свойства: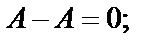
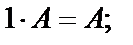
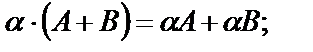
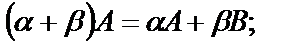
 .
.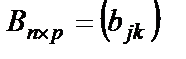 называется матрица
называется матрица 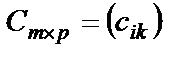 такая, что
такая, что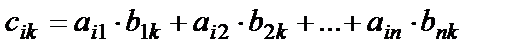 , (12)
, (12)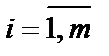 ,
, 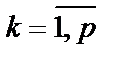 .
.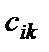 полезно помнить в виде правила:
полезно помнить в виде правила: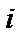 - ю строку, в матрице
- ю строку, в матрице 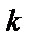 -й столбец.
-й столбец.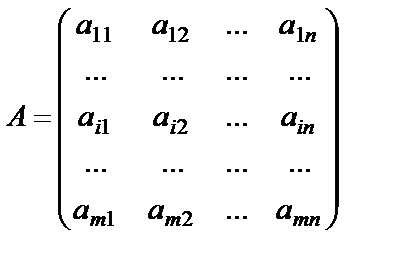 ,
, 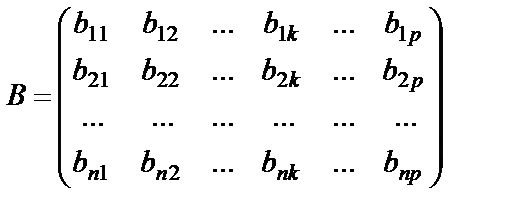 .
.
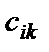 матрицы
матрицы 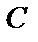 , расположенный на пересечении i-й строки и k -го столбца, надо каждый элемент i -й строки матрицы
, расположенный на пересечении i-й строки и k -го столбца, надо каждый элемент i -й строки матрицы 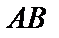 и
и 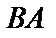 всегда существуют.
всегда существуют.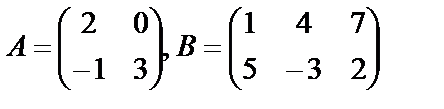 .
.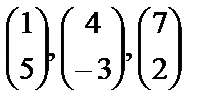 .
.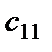 находим как сумму произведений элементов первой строки матрицы
находим как сумму произведений элементов первой строки матрицы 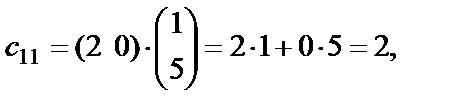
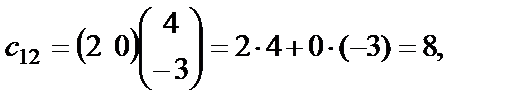
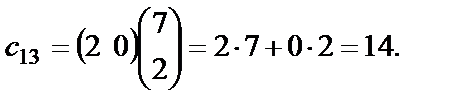
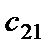 ,
, 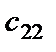 ,
, 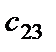 фиксируем вторую строку матрицы
фиксируем вторую строку матрицы 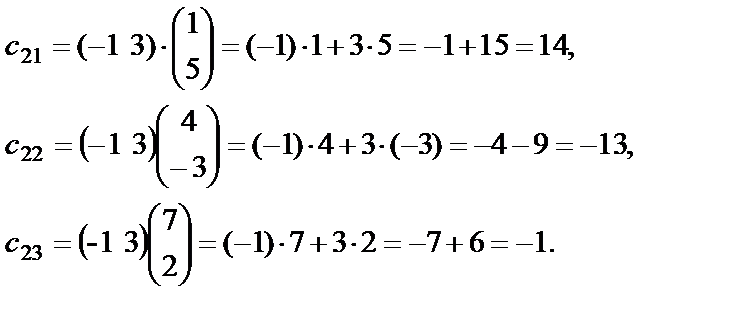
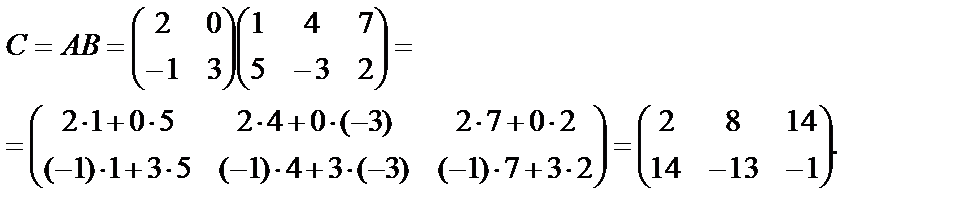
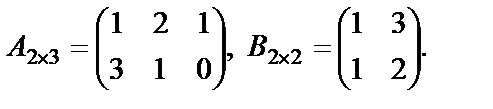 Найти
Найти 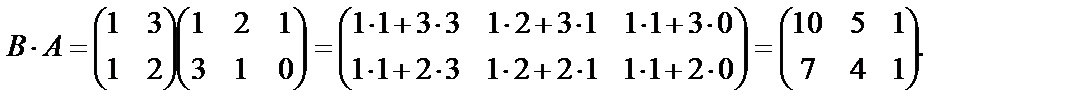 Матрицы
Матрицы 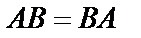 .
.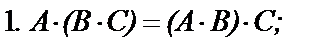
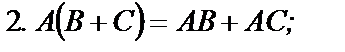
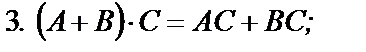
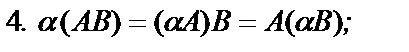
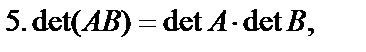 если указанные суммы и произведения матриц имеют смысл.
если указанные суммы и произведения матриц имеют смысл.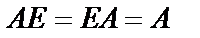 .
.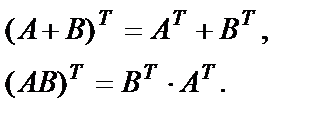
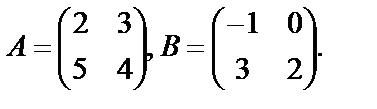
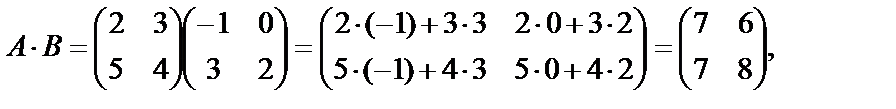
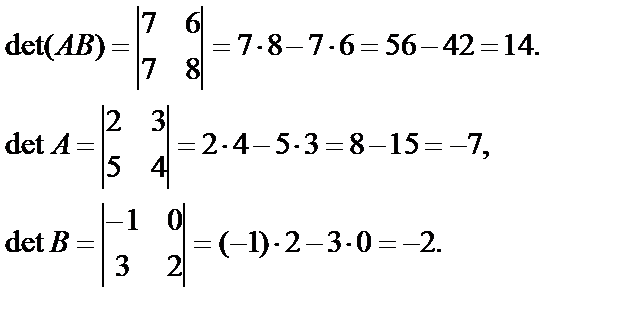
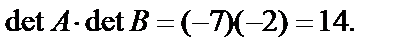
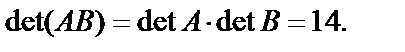
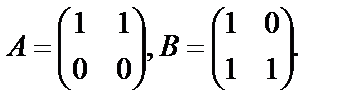
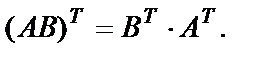
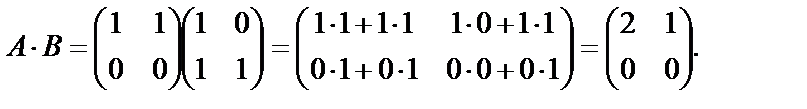
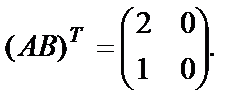

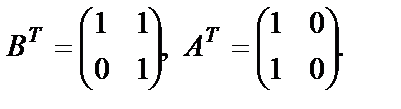
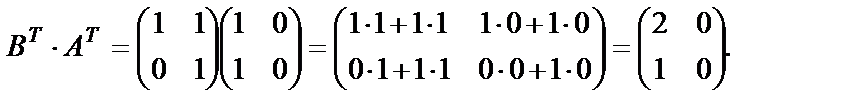
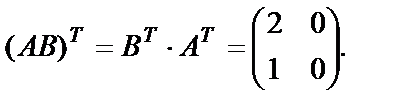
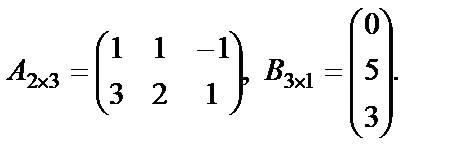
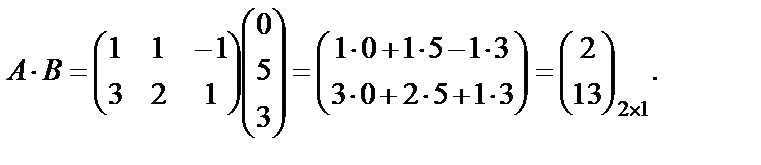
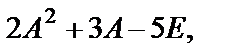 если
если 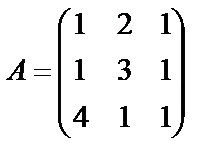 , Е - единичная матрица третьего порядка.
, Е - единичная матрица третьего порядка.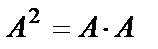 . Найдем
. Найдем 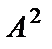 :
: =
= 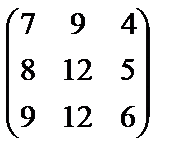 ,
, 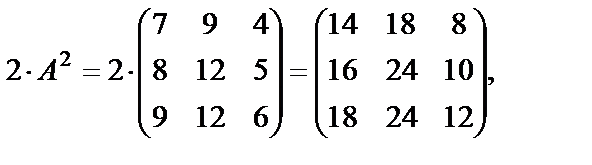
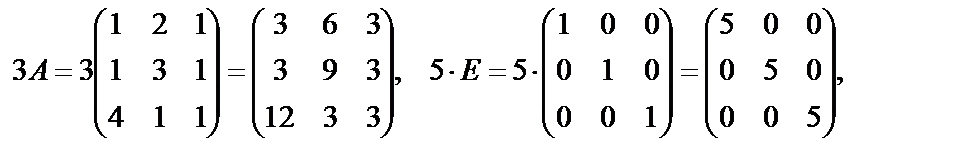
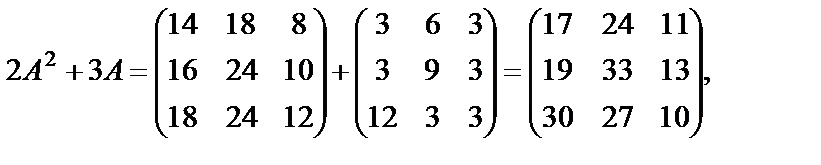
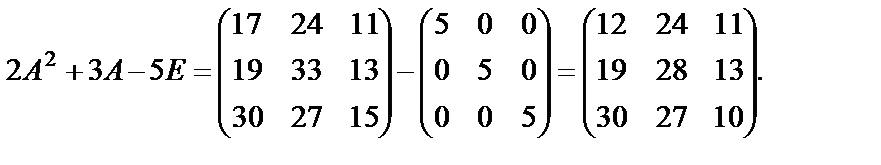
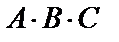 , если оно определено, где
, если оно определено, где 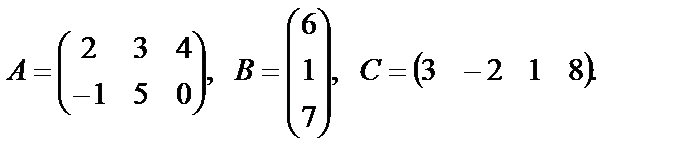
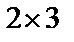 , размер матрицы
, размер матрицы 
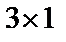 . Так как число столбцов матрицы
. Так как число столбцов матрицы 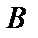 (3), то произведение
(3), то произведение 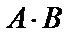 определено, в результате получим матрицу размера
определено, в результате получим матрицу размера 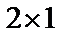 .
.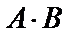 (1) совпадает с числом строк матрицы
(1) совпадает с числом строк матрицы 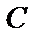 (1), таким образом, произведение
(1), таким образом, произведение 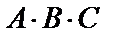 определено, получаемая матрица будет размера
определено, получаемая матрица будет размера 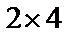 .
.