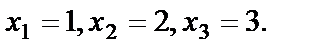Матричный метод решения систем
Рассмотрим систему n линейных уравнений с n неизвестными
Основная матрица системы Обозначим
которое называется матричным уравнением. Решим матричное уравнение. Умножим обе части уравнения (22) слева на
Равенство (23) называется решением матричного уравнения (22). Таким образом, чтобы решить систему уравнений (21) матричным методом, где Пример 34. Решить систему уравнений матричным методом
Решение. Выпишем основную матрицу системы
Проверим, является ли матрица А невырожденной:
значит матрица Найдем алгебраические дополнения элементов матрицы
Составим матрицу
По формуле (15) получим матрицу
Найдем решение данной системы уравнений по формуле (23)
Пример 35. Матричным методом решить систему уравнений
Решение. Запишем основную матрицу системы
и вычислим определитель этой матрицы В полученном определителе элементы первой строки пропорциональны соответствующим элементам второй строки, тогда по свойству 6 определителей Матрица
|
(21)
.
, 
. Пусть 
, то есть матрица А невырожденная. Тогда систему (21) можно представить в виде уравнения
(22)
. Получим 
, а так как 
, 
, тогда
(23)
является невырожденной, поэтому обратная матрица 
, присоединенную к матрице А:
то есть 
