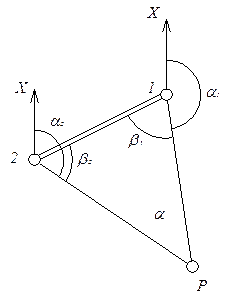Прямая геодезическая засечка

Прямая геодезическая засечка применяется для определения координат дополнительной точки на основании двух исходных пунктов с известными координатами на местности, неудобной для производства линейных измерений. Для этого достаточно, установив теодолит последовательно на исходных пунктах 1 и 2 (рис. 12.1), измерить горизонтальные углы b₁ и b₂ между исходной стороной 1-2 и направлениями на определяемую точку Р.

Прямая засечка может быть использована также для привязки теодолитных или тахеометрических ходов к пунктам геодезической опорной сети, для чего необходимо измерить дополнительно примычной угол j₁ (или j₂) на определяемой точке.

Вычисление координат искомой точки может быть выполнено по формулам Юнга и Гаусса, не требующим предварительного решения треугольника. В этом случае должен соблюдаться определенный порядок нумерации исходных пунктов, отвечающих правилу: если встать в середине линии между исходными пунктами лицом к искомому пункту Р, то исходный пункт. Находящийся слева будет первым, а справа – вторым. Тогда координаты точки Р определятся по формулам котангенсов внутренних углов треугольника (формулам Юнга):

Рисунок 12.1 – Прямая геодезическая засечка

Координаты определяемой точки Р могут быть также получены по формулам тангенсов и котангенсов дирекционных углов (формулам Гаусса). Если значение одного из дирекционных углов будет близким к 0⁰ или 180⁰, то вычисление координат точки Р удобно производить по формулам тангенсов дирекционных углов:

В случае, когда значение одного из дирекционных углов будет близким к 90⁰ или 270⁰, вычисление по вышеуказанным формулам становится неудобным вследствие большой величины тангенса этого дирекционного угла. В этом случае выгодно пользоваться формулами котангенсов дирекционных углов: