Задания для самостоятельной работы. 3.1.Длинный прямой проводник с током J и П-образный проводник с подвижной перемычкой расположены в одной плоскости
3.4. В цепи, состоящей из заряженного конденсатора емкости С0 и катушки индуктивности L, замыкают ключ К. По какому закону должна изменяться во времени емкость конденсатора, чтобы ток в цепи нарастал прямо пропорционально времени?
3.5. Найти собственные частоты колебаний w1,2 в двух индуктивно связанных контурах с емкостями С 1, С 2, индуктивностями L 1, L 2 и коэффициентом взаимной индукции L 12.
3.6. Плоский контур с параметрами R, L, C и площадью S вращается с угловой скоростью w в постоянном магнитном поле В 0 вокруг оси, лежащей в плоскости контура и перпендикулярной В 0. Определить средний тормозящий момент áМñ;, приложенный к контуру.
3.7. Определить частоты собственных колебаний контуров, связь между которыми носит емкостной характер (Z = - i/wC).
3.8. Определить частоты собственных колебаний индуктивно связанных контуров (Z = iwL).
3.9. В контур с индуктивностью L 1, емкостью C 1 и сопротивлением R 1 включена ЭДС e(t) = e0eiwt . С этим контуром индуктивно связан второй контур, параметры которого L 2, C 2 и R 2. Коэффициент взаимной индукции L 12. Определить токи J 1 и J 2 в обоих контурах.
3.10. К цепочке, состоящей из последовательно соединенных сопротивления R и индуктивности L, прикладывается прямоугольный импульс напряжения U(t) = U0 при 0 £ t £ T и U(t) = 0 при t > T. Определить ток в цепочке как функцию времени.
3.11. Цепь состоит из плоского конденсатора емкости С (расстояние между пластинами d) и сопротивления R. Между пластинами конденсатора требуется создать поле, которое линейно возрастает от 0 до Е 0 за время Т, а затем за то же время линейно убывает до нуля. Определить форму импульса напряжения, которое нужно подать на вход цепи.
3.12. В длинном прямом соленоиде с радиусом a и числом витков на единицу длины n протекает ток, изменяющийся с постоянной скоростью
3.13. В колебательном контуре с параметрами R, L и C совершаются затухающие колебания. В определенный момент времени амплитуда колебаний была равной J 1, а спустя некоторое время стала равной J 2. Какое количество теплоты выделилось в контуре за это время?
3.14. На длинный соленоид с радиусом сечения а плотно надето тонкое проволочное кольцо в изоляции, причем одна половина кольца имеет сопротивление в h раз больше, чем вторая. Индукция магнитного поля соленоида меняется по закону B = bt, где b = const. Определить модуль напряженности электрического поля в кольце.
3.15. Магнитный поток через поверхность неподвижного контура с сопротивлением R изменяется в течение времени t по закону Ф = at(t - t). Найти количество теплоты, выделившееся в контуре за это время. Индуктивностью контура пренебречь.
3.16. Длинный прямой соленоид имеет n витков на единицу длины. По нему течет ток J = J 0sin wt. Определить плотность тока смещения как функцию расстояния r от оси соленоида. Радиус сечения соленоида R.
3.18. Найти частоту колебаний контура, показанного на рис. Проанализировать, при каком соотношении между R, L и C колебания в контуре возможны.
3.19. Имеются два колебательных контура с конденсаторами одинаковой емкости. При каком соотношении между индуктивностями и активными сопротивлениями катушек частоты колебаний контуров будут одинаковыми?
ОТВЕТЫ К ЗАДАНИЯМ 3.1. 3.4. 3.6. 3.7. 3.8. 3.9.
3.10.
3.11. 3.12. 3.14.
3.18.
|

 3.1. Длинный прямой проводник с током J и П-образный проводник с подвижной перемычкой расположены в одной плоскости, как показано на рис. Перемычку, длина которой l и сопротивление R, перемещают вправо со скоростью v. Найти ток, индуцируемый в контуре, как функцию расстояния r между перемычкой и прямым проводником.
3.1. Длинный прямой проводник с током J и П-образный проводник с подвижной перемычкой расположены в одной плоскости, как показано на рис. Перемычку, длина которой l и сопротивление R, перемещают вправо со скоростью v. Найти ток, индуцируемый в контуре, как функцию расстояния r между перемычкой и прямым проводником. 3.2. Проволочный контур, ограничивающий полукруг радиуса а, находится на границе однородного магнитного поля с индукцией В. В момент t = 0 контур начинают вращать с постоянным угловым ускорением b вокруг оси О, совпадающей с линией вектора
3.2. Проволочный контур, ограничивающий полукруг радиуса а, находится на границе однородного магнитного поля с индукцией В. В момент t = 0 контур начинают вращать с постоянным угловым ускорением b вокруг оси О, совпадающей с линией вектора  на границе поля. Найти ЭДС индукции в контуре как функцию времени. Показать графически эту зависимость.
на границе поля. Найти ЭДС индукции в контуре как функцию времени. Показать графически эту зависимость.
 3.3. Проводник АС массы m скользит без трения по двум длинным проводящим рельсам, расположенным на расстоянии l друг от друга. Рельсы с одной стороны замкнуты на сопротивление R, как показано на рис. Система находится в однородном магнитном поле индукции В, перпендикулярном плоскости контура. В момент времени t = 0 проводнику АС сообщают скорость v0. Найти расстояние, пройденное стержнем АС до остановки, а также количество теплоты, которое выделится при этом на сопротивлении R.
3.3. Проводник АС массы m скользит без трения по двум длинным проводящим рельсам, расположенным на расстоянии l друг от друга. Рельсы с одной стороны замкнуты на сопротивление R, как показано на рис. Система находится в однородном магнитном поле индукции В, перпендикулярном плоскости контура. В момент времени t = 0 проводнику АС сообщают скорость v0. Найти расстояние, пройденное стержнем АС до остановки, а также количество теплоты, которое выделится при этом на сопротивлении R.
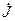 А/с. Определить напряженность электрического поля как функцию расстояния от оси соленоида r.
А/с. Определить напряженность электрического поля как функцию расстояния от оси соленоида r. 3.17. В начальный момент времени конденсатор С 0 в цепи, показанной на рис., заряжен до напряжения U 0, ключ К разомкнут. Найти зависимость от времени напряжения U 1 на конденсаторе С 0 и напряжения U 2 на конденсаторе С после замыкания ключа К.
3.17. В начальный момент времени конденсатор С 0 в цепи, показанной на рис., заряжен до напряжения U 0, ключ К разомкнут. Найти зависимость от времени напряжения U 1 на конденсаторе С 0 и напряжения U 2 на конденсаторе С после замыкания ключа К.

 . 3.2.
. 3.2.  . 3.3.
. 3.3.  .
. . 3.5.
. 3.5. 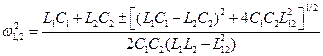 .
.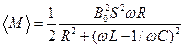 .
.
 .
. , где
, где 
 , i - мнимая единица.
, i - мнимая единица. при 0 £ t £ T,
при 0 £ t £ T,  при t ³ T.
при t ³ T.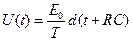 при 0 £ t £ T,
при 0 £ t £ T,  при T £ t £ 2T.
при T £ t £ 2T.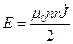 при r £ a,
при r £ a,  при r ³ a. 3.13.
при r ³ a. 3.13.  .
.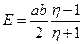 . 3.15.
. 3.15.  . 3.16.
. 3.16.  при r £ R,
при r £ R,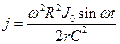 при r ³ R. 3.17.
при r ³ R. 3.17.  ,
, , где
, где  .
. . 3.19.
. 3.19. 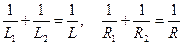 .
.


