Примеры решения задач. Пример.Диэлектрический слой с проницаемостью e2, ограниченный плоскостями z = 0 и z = a, разделяет диэлектрические среды с e1 и e3(m1 = m2 = m3 = 1)
Пример. Диэлектрический слой с проницаемостью e2, ограниченный плоскостями z = 0 и z = a, разделяет диэлектрические среды с e 1 и e 3(m 1 = m 2 = m 3 = 1). На слой из области z < 0 нормально падает плоская монохроматическая линейно поляризованная электромагнитная волна. При какой толщине слоя отражение будет минимальным? При каком соотношении между e 1, e 2 и e 3 при этом отражения не будет?
При этом электрическая и магнитная составляющие падающей электромагнитной волы могут быть представлены в виде:
На границе z = 0 волна частично отражается в первую среду и частично проходит во вторую. Составляющие отраженной волны могут быть представлены в виде:
причем, т.к. k 1 ® - k 1, то в соответствии с (4.9)
Прошедшая волна на границе z = a также частично отражается и частично проходит в третью среду. Повторяя рассуждения, для второй среды получаем
В третьей среде имеется только прошедшая волна с составляющими
В записанных выражениях для электромагнитных полей
Поставленная задача сводится к нахождению коэффициента отражения плоской эдектромагнитной волне связаны с амплитудами электрических составляющих, то неизвестными являются лишь четыре амплитуды -
быть выражены через амплитуду падающей волны Условия непрерывности тангенциальных составляющих векторов напряженности электрического и магнитного полей на границах z = 0 и z = a приводят к системе уравнений 1) 3) Из уравнений 1) и 2) получаем
Из уравнений 3) и 4)
где
Тогда искомый коэффициент отражения Исследование полученного выражения на экстремум (дифференцирование по а) показывает, что минимуму коэффициента отражения соответствует условие Т.к. k 2 ¹ 0, то это условие выполняется при Таким образом, при толщине слоя, равной или кратной четверти длины волны, коэффициент отражения обращается в ноль при
|

 Пусть вектор
Пусть вектор  падающей волны лежит в плоскости падения, т.е.
падающей волны лежит в плоскости падения, т.е.  ; при этом магнитная составляющая падающей волны
; при этом магнитная составляющая падающей волны  - см. рис.4.2, а связь между ними выражается соотношением
- см. рис.4.2, а связь между ними выражается соотношением .
. и
и  .
.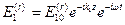 и
и  ,
, . Полное волновое поле в первой среде представляет собой суперпозицию падающей и отраженной волн, т.е.
. Полное волновое поле в первой среде представляет собой суперпозицию падающей и отраженной волн, т.е. и
и 
 ,
,  ,
, ,
,  ,
,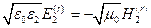 и
и  .
. и
и  .
. .
. , т.е. к нахождению отношения амплитуды отраженной волны к амплитуде падающей волны в первой среде. Т.к. амплитуды магнитных составляющих в
, т.е. к нахождению отношения амплитуды отраженной волны к амплитуде падающей волны в первой среде. Т.к. амплитуды магнитных составляющих в , которые могут
, которые могут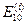 с помощью граничных условий.
с помощью граничных условий. , 2)
, 2)  ,
, , 4)
, 4)  .
. , где
, где 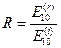 - амплитудный коэффициент отражения, и
- амплитудный коэффициент отражения, и .
. . Подстановка этого отношения в выражение для R позволяет записать его в виде
. Подстановка этого отношения в выражение для R позволяет записать его в виде ,
,
 .
. .
. .
. , т.е при
, т.е при 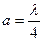 , где l - длина волны. Подстановка
, где l - длина волны. Подстановка 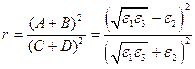 .
. . Полученные результаты остаются справедливыми и при любой другой поляризации электромагнитной волны при условии нормального падения, в чем нетрудно убедиться непосредственными расчетами, аналогичными проведенным.
. Полученные результаты остаются справедливыми и при любой другой поляризации электромагнитной волны при условии нормального падения, в чем нетрудно убедиться непосредственными расчетами, аналогичными проведенным.


