4.1.  . 4.2.
. 4.2. 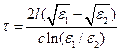 . 4.3.
. 4.3.  .
.
4.4. ei =  . 4.5.
. 4.5.  . 4.7.
. 4.7.  .
.
4.8.  .
.
4.9.  . 4.10.
. 4.10.  .
.
4.11.  . 4.12.
. 4.12.  .
.
4.13.  .
.
4.14. Поляризация эллиптическая с полуосями  ,
,
 , повернутыми на угол a по отношению к исходным поляризациям такой, что
, повернутыми на угол a по отношению к исходным поляризациям такой, что  .
.
Элементы теории излучения
4.17.  . 4.18.
. 4.18. 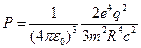 .
.
4.19.  . 4.20.
. 4.20.  .
.
4.21.  . 4.22.
. 4.22.  .
.
4.23. 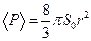 . 4.24.
. 4.24.  . 4.25.
. 4.25.  . 4.26.
. 4.26.  .
.
4.27.  . 4.28.
. 4.28. 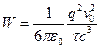 .
.
ВАРИАНТЫ ЗАДАНИЙ
|
№ п/п
| 1. ЭЛЕКТРОСТАТИКА
| 2. СТАЦИОНАРНЫЕ ПОЛЯ. МАГНИТОСТАТИКА
| 3.КВАЗИ-
СТАЦИО-
НАРНЫЕ ПОЛЯ
| 4. ЭЛЕКТРО-
МАГН. ВОЛНЫ.
ИЗЛУЧЕНИЕ
|
| 1.1
| 1.2
| 1.3
| 1.4
| 1.5
| 1.6
| 2.1
| 2.2
| 2.3
| 2.4
| 4.1
| 4.2
|
|
| 1.2
| 1.17
| 1.37
| 1.59
| 1.77
| 1.103
| 2.3
| 2.29
| 2.44
| 2.58
| 3.1
| 4.1
| 4.17
|
|
| 1.1
| 1.32
| 1.38
| 1.60
| 1.78
| 1.97
| 2.4
| 2.28
| 2.45
| 2.57
| 3.2
| 4.2
| 4.18
|
|
| 1.3
| 1.18
| 1.39
| 1.61
| 1.79
| 1.98
| 2.5
| 2.30
| 2.46
| 2.59
| 3.3
| 4.3
| 4.19
|
 4 4
| 1.4
| 1.22
| 1.40
| 1.63
| 1.80
| 1.99
| 2.6
| 2.31
| 2.47
| 2.60
| 3.4
| 4.4
| 4.20
|
|
| 1.6
| 1.27
| 1.41
| 1.64
| 1.81
| 1.100
| 2.7
| 2.32
| 2.48
| 2.61
| 3.5
| 4.5
| 4.21
|
|
| 1.5
| 1.28
| 1.43
| 1.65
| 1.84
| 1.101
| 2.8
| 2.33
| 2.49
| 2.62
| 3.6
| 4.6
| 4.22
|
|
| 1.8
| 1.29
| 1.44
| 1.66
| 1.83
| 1.102
| 2.9
| 2.34
| 2.50
| 2.64
| 3.7
| 4.7
| 4.23
|
|
| 1.10
| 1.23
| 1.45
| 1.67
| 1.86
| 1.103
| 2.10
| 2.35
| 2.51
| 2.65
| 3.8
| 4.8
| 4.24
|
|
| 1.11
| 1.19
| 1.46
| 1.69
| 1.87
| 1.104
| 2.11
| 2.36
| 2.52
| 2.66
| 3.9
| 4.9
| 4.25
|
|
| 1.12
| 1.20
| 1.50
| 1.70
| 1.91
| 1.105
| 2.12
| 2.38
| 2.53
| 2.67
| 3.10
| 4.10
| 4.26
|
|
| 1.13
| 1.21
| 1.48
| 1.71
| 1.89
| 1.106
| 2.13
| 2.37
| 2.54
| 2.69
| 3.11
| 4.11
| 4.27
|
|
| 1.14
| 1.25
| 1.49
| 1.72
| 1.90
| 1.107
| 2.14
| 2.39
| 2.55
| 2.74
| 3.12
| 4.12
| 4.28
|
|
| 1.15
| 1.36
| 1.51
| 1.73
| 1.91
| 1.108
| 2.16
| 2.40
| 2.44
| 2.75
| 3.13
| 4.13
| 4.29
|
|
| 1.10
| 1.24
| 1.52
| 1.74
| 1.92
| 1.109
| 2.17
| 2.41
| 2.45
| 2.70
| 3.14
| 4.14
| 4.17
|
|
| 1.9
| 1.34
| 1.53
| 1.75
| 1.93
| 1.110
| 2.18
| 2.42
| 2.46
| 2.71
| 3.15
| 4.15
| 4.18
|
|
| 1.16
| 1.26
| 1.54
| 1.76
| 1.94
| 1.111
| 2.19
| 2.43
| 2.47
| 2.72
| 3.16
| 4.16
| 4.19
|
|
| 1.1
| 1.33
| 1.55
| 1.68
| 1.95
| 1.112
| 2.21
| 2.29
| 2.48
| 2.73
| 3.17
| 4.3
| 4.20
|
|
| 1.4
| 1.35
| 1.56
| 1.71
| 1.89
| 1.113
| 2.22
| 2.30
| 2.49
| 2.74
| 3.18
| 4.6
| 4.21
|
|
| 1.12
| 1.30
| 1.52
| 1.70
| 1.93
| 1.114
| 2.23
| 2.33
| 2.50
| 2.75
| 3.19
| 4.11
| 4.22
|
|
| 1.15
| 1.31
| 1.49
| 1.65
| 1.85
| 1.104
| 2.20
| 2.34
| 2.51
| 2.68
| 3.2
| 4.12
| 4.23
|
ПРИЛОЖЕНИЕ 1. ОПЕРАТОРЫ ТЕОРИИ ПОЛЯ В КРИВОЛИНЕЙНЫХ
ОРТОГОНАЛЬНЫХ КООРДИНАТАХ
При решении физических задач, обладающих той или иной симметрией, приходится пользоваться различными криволинейными ортогональными координатами. Краткое описание векторных соотношений и операторов теории поля в различных ортогональных координатах будет полезным как для усвоения теоретического материала, так и при выполнении предлагаемых заданий.
П1.1. Декартовы координаты
С декартовыми координатами x, y и z связана правая тройка единичных ортогональных векторов 
 и
и  . Элементы длины, площади и объема имеют вид:
. Элементы длины, площади и объема имеют вид:
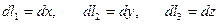
 ,
,
 .
.
Векторный оператор «набла» и оператор Лапласа записываются следующим образом
 ,
,
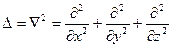 .
.
При этом градиент скалярной функции j
 ,
,
дивергенция векторной функции 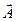
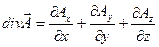 ,
,
и ротор векторной функции 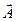
 .
.

 . 4.2.
. 4.2. 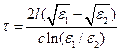 . 4.3.
. 4.3.  .
. . 4.5.
. 4.5.  . 4.7.
. 4.7.  .
. .
. . 4.10.
. 4.10.  .
. . 4.12.
. 4.12.  .
. .
. ,
, , повернутыми на угол a по отношению к исходным поляризациям такой, что
, повернутыми на угол a по отношению к исходным поляризациям такой, что  .
. . 4.18.
. 4.18. 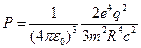 .
. . 4.20.
. 4.20.  .
. . 4.22.
. 4.22.  .
.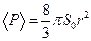 . 4.24.
. 4.24.  . 4.25.
. 4.25.  . 4.26.
. 4.26.  .
. . 4.28.
. 4.28. 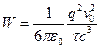 .
. 4
4

 и
и  . Элементы длины, площади и объема имеют вид:
. Элементы длины, площади и объема имеют вид: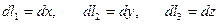
 ,
, .
. ,
,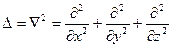 .
. ,
,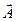
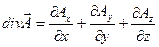 ,
, .
.


