Примеры решения задач. Пример 1.Определить время, за которое электрон атома водорода в модели Резерфорда упадет на ядро вследствие потери энергии на излучение
Пример 1. Определить время, за которое электрон атома водорода в модели Резерфорда упадет на ядро вследствие потери энергии на излучение. Первоначальный радиус орбиты электрона принять равным Боровскому радиусу а.
где е – величина заряда электрона, Т.к. масса ядра много больше массы электрона, то центр масс атома совпадает с центром ядра. Поэтому в системе центра масс дипольный момент атома совпадает с дипольным моментом электрона и равен Индукция магнитного поля дипольного излучения электрона
Энергия излучения, протекающая в единицу времени через площадку
В последнем выражении
Для электрона в атоме
Следовательно, энергия, излучаемая электроном атома в единицу времени, равна:
Для определения времени жизни атома найдем полную энергию электрона, находящегося на круговой орбите радиуса r. Учтем, что
Разделяя переменные, получаем
При выполнении интегрирования учтем, что в начальный момент времени энергия электрона
Выполняя интегрирование, получаем
Пример 2. Определить среднюю мощность излучения рамки с током Т.к. электрический дипольный момент рамки с током равен 0, то поле излучения определяется ее магнитным моментом
Здесь Плотность потока энергии
Тогда энергия, протекающая в единицу времени через площадку
Интегрирование по телесному углу приводит к
Так же, как и в предыдущем примере, при нахождении мощности излучения рамки в полученном выражении время задержки t можно опустить. Тогда средняя за период мощность излучения рамки с током будет равной
В соответствии с выражением (4.23) для электрического дипольного момента, изменяющегося по гармоническому закону, имеем
|

 Электрон в атоме движется под действием кулоновской силы, обеспечивающей центростремительное ускорение:
Электрон в атоме движется под действием кулоновской силы, обеспечивающей центростремительное ускорение: ,
, - его радиус-вектор относительно ядра (рис. 4.3).
- его радиус-вектор относительно ядра (рис. 4.3).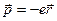 .
. , где r ¢ - расстояние от ядра до точки наблюдения, а плотность потока энергии излучения
, где r ¢ - расстояние от ядра до точки наблюдения, а плотность потока энергии излучения .
. на сферической поверхности r ¢ = const,
на сферической поверхности r ¢ = const, .
.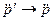 , т.к. из закона сохранения энергии следует, что поток энергии в единицу времени через любую поверхность r ¢ = const остается постоянным и не зависит от времени задержки t. Выполняя интегрирование по полному телесному углу, получаем
, т.к. из закона сохранения энергии следует, что поток энергии в единицу времени через любую поверхность r ¢ = const остается постоянным и не зависит от времени задержки t. Выполняя интегрирование по полному телесному углу, получаем .
. и
и  .
. .
. и
и 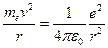 . Поэтому кинетическая энергия электрона в атоме
. Поэтому кинетическая энергия электрона в атоме 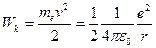 . С другой стороны, потенциальная энергия электрона
. С другой стороны, потенциальная энергия электрона  . Следовательно, полная энергия
. Следовательно, полная энергия  и является функцией расстояния электрона от ядра r. Тогда полученное выражение для энергии, теряемой на излучение в единицу времени, можно преобразовать к виду:
и является функцией расстояния электрона от ядра r. Тогда полученное выражение для энергии, теряемой на излучение в единицу времени, можно преобразовать к виду: .
. .
. , а падению электрона на ядро соответствует энергия W¢ ® - ¥. Тогда
, а падению электрона на ядро соответствует энергия W¢ ® - ¥. Тогда .
. .
.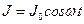 . Площадь рамки S. Какой длины должно быть плечо l электрического диполя зарядом
. Площадь рамки S. Какой длины должно быть плечо l электрического диполя зарядом  q
q  , чтобы его мощность излучения равнялась мощности излучения рамки?
, чтобы его мощность излучения равнялась мощности излучения рамки? :
:
 .
.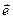 - вектор нормали к рамке с током, а
- вектор нормали к рамке с током, а  - единичный вектор в направлении на точку наблюдения поля (см. рис. 4.4).
- единичный вектор в направлении на точку наблюдения поля (см. рис. 4.4). .
. , будет равной
, будет равной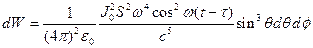 .
. .
. .
.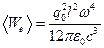 . Сравнивая результаты, приходим к выводу, что электрический диполь излучает ту же мощность, что и рамка с током при длине плеча диполя
. Сравнивая результаты, приходим к выводу, что электрический диполь излучает ту же мощность, что и рамка с током при длине плеча диполя 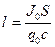 . Для гармонически изменяющегося заряда q такого, что
. Для гармонически изменяющегося заряда q такого, что  , получаем
, получаем  , где l - длина волны электромагнитного излучения.
, где l - длина волны электромагнитного излучения.


