Краткие теоретические сведения. В отсутствие зарядов и токов, но при наличии переменных электрических и магнитных полей уравнения Максвелла принимают вид
В отсутствие зарядов и токов, но при наличии переменных электрических и магнитных полей уравнения Максвелла принимают вид 1) 2) а поле, описываемое этими уравнениями, называется свободным электромагнитным полем. Система четырех дифференциальных уравнений первого порядка (4.1) может быть приведена к системе двух дифференциальных уравнений второго порядка, имеющих вид волновых уравнений:
Следовательно, свободное электромагнитное поле может существовать лишь в форме электромагнитной волны, распространяющей в однородной и изотропной среде со скоростью
В вакууме (ε; = 1, μ; = 1) скорость распространения электромагнитных волн равна скорости света
В общем случае волна – это возбуждение, распространяющееся в среде с постоянной скоростью, определяемой свойствами этой среды. Геометрическое место точек, значение возмущения в которых одинаково, называется волновой поверхностью (поверхностью равных фаз, фронтом волны). По форме фронта вводятся две основные модели волны - плоская и сферическая: фронтом плоской волны является плоскость, а фронтом сферической – сфера. Плоская электромагнитная волна в вакууме может быть представлена в виде двух составляющих:
где Уравнение сферической электромагнитной волны, распространяющейся в вакууме, имеет общий вид:
В уравнениях (4.7)и (4.8) с – фазовая скорость волны, совпадающая со скоростью света. Векторы
Волны, в которых электрическая и магнитная составляющие изменяются по гармоническому закону называются монохроматическими. Если при этом направления, вдоль которых происходят колебания векторов
Здесь В общем случае возмущения произвольной формы электромагнитная волна может быть представлена суперпозицией плоских линейно поляризованных монохроматических волн. При распространении электромагнитной волны в непроводящей среде с диэлектрической проницаемостью e и магнитной проницаемостью mв уравнениях (4.7) – (4.10) следует заменить с на
В плоской электромагнитной волне плотность энергии электрической и магнитной составляющих равны. Поэтому
Плотность потока электромагнитной энергии (интенсивность волны) определяется следующими выражениеми:
В проводящей среде электромагнитные волны затухают, что отражается введением комплексного волнового вектора k* = k¢ + ik¢¢; в (4.10). Комплексность волнового вектора связана с комплексностью диэлектрической проницаемости, наличие мнимой части которой обусловлено электропроводностью среды:
Действительная и мнимая части k * связаны с материальными константами среды и зависят от частоты:
Рассмотренные решения уравнений Максвелла (4.1) представляют собой решения системы однородных волновых уравнений. При наличии переменных зарядов и токов ставится задача нахождения частных решений полной системы уравнений Максвелла
удовлетворяющих заданному распределению зарядов и токов. С использованием калибровки Лоренца для скалярного и векторного потенциалов
уравнения (4.16) преобразуются в неоднородные волновые уравнения относительно этих потенциалов:
Частными решениями этих уравнений являются запаздывающие потенциалы (для простоты записей принимаем e = 1 и m = 1):
Здесь, по-прежнему, Если полный заряд системы зарядов равен нулю, а электрический дипольный момент отличен от нуля, то на больших расстояниях в волновой зоне (r >>l >> l~ r¢;; l - линейный размер системы)
где точка над С радиационными потенциалами связаны напряженность электрического и индукция магнитного поля излучения диполя:
Т.к. сферическую волну на больших расстояниях от источника можно рассматривать как плоскую, то плотность потока энергии дипольного излучения, равная
Полная энергия, теряемая диполем в единицу времени (мощность излучения) может быть получена интегрированием
Если электрический дипольный момент системы зарядов равен нулю, но отличен от нуля магнитный момент, то поле излучения в волновой зоне определяется этим моментом и описывается выражениями:
|

 , 2)
, 2)  ,
, , 3)
, 3)  , (4.1)
, (4.1) , (4.3)
, (4.3) . (4.4)
. (4.4) . (4.5)
. (4.5) (4.6)
(4.6) , (4.7)
, (4.7) - единичный вектор в направлении распространения волны.
- единичный вектор в направлении распространения волны.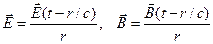 . (4.8)
. (4.8) и
и  в плоской волне взаимно перпендикулярны и образуют правую тройку векторов. Для электромагнитной волны в вакууме
в плоской волне взаимно перпендикулярны и образуют правую тройку векторов. Для электромагнитной волны в вакууме . (4.9)
. (4.9)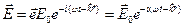 , (4.10а)
, (4.10а) . (4.10б)
. (4.10б)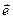 и
и 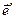 - векторы поляризации, Е0 и B0 – амплитуды колебаний напряженности электрического и индукции магнитного полей, w - циклическая частота колебаний,
- векторы поляризации, Е0 и B0 – амплитуды колебаний напряженности электрического и индукции магнитного полей, w - циклическая частота колебаний,  - волновой вектор, причем
- волновой вектор, причем 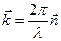 ,где
,где  - длина волны. При этом следует помнить, что физический смысл имеют лишь действительные части (4.10а) и (4.10б).
- длина волны. При этом следует помнить, что физический смысл имеют лишь действительные части (4.10а) и (4.10б). , а между величинами Е, В, D и Н существует простая связь:
, а между величинами Е, В, D и Н существует простая связь: . (4.11)
. (4.11) . (4.12)
. (4.12)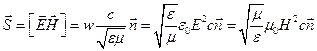 . (4.13)
. (4.13) . (4.14)
. (4.14) . (4.15)
. (4.15) ,
, , (4.16)
, (4.16)
 (4.17а)
(4.17а) . (4.17б)
. (4.17б) , (4.18)
, (4.18) . (4.19)
. (4.19) , а R/c – время, в течение которого распространяющееся со скоростью с поле достигает точки наблюдения. Таким образом, поле в точке наблюдения в момент времени t определяется значениями зарядов и токов в различные предшествующие моменты времени.
, а R/c – время, в течение которого распространяющееся со скоростью с поле достигает точки наблюдения. Таким образом, поле в точке наблюдения в момент времени t определяется значениями зарядов и токов в различные предшествующие моменты времени. , (4.20)
, (4.20) означает дифференцирование по времени, а штрих подразумевает, что значение дипольного момента берется в момент времени (t - t). Задержка t = r/c представляет собой время, в течение которого поле распространяется от системы зарядов как целого до точки наблюдения. Из (4.20) видно, что электромагнитное поле электрического диполя в волновой зоне представляет собой сферическую волну. Поэтому величины j и
означает дифференцирование по времени, а штрих подразумевает, что значение дипольного момента берется в момент времени (t - t). Задержка t = r/c представляет собой время, в течение которого поле распространяется от системы зарядов как целого до точки наблюдения. Из (4.20) видно, что электромагнитное поле электрического диполя в волновой зоне представляет собой сферическую волну. Поэтому величины j и  в (4.20) называются радиационными потенциалами.
в (4.20) называются радиационными потенциалами. . (4.21)
. (4.21)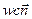 , может быть преобразована к виду (см. рис.4.1):
, может быть преобразована к виду (см. рис.4.1):
 (4.22)
(4.22) по полному телесному углу, т.е. всем значениям углов q и f:
по полному телесному углу, т.е. всем значениям углов q и f: . (4.23)
. (4.23) . (4.24)
. (4.24)


