Задание 4.2.
1. Разложить в степенной ряд > f(x)=series(exp(-x)*sqrt(x+1), x=0, 5);
2. Построить на одном рисунке графики интеграла ошибок > taylor(erf(x),x,8): p:=convert(%,polynom);
> plot({erf(x),p},x=-2..2,thickness=[2,2], linestyle=[1,3], color=[red,green]);
Пунктирной линей изображен график ряда Тейлора, а сплошной – самой функции. 3. Разложить > readlib(mtaylor): > f=mtaylor(sin(x^2+y^2), [x=0,y=0], 7);
Создание собственных процедур. Разложение функции в ряд Фурье. В Maple имеется возможность создавать собственные процедуры. Процедура начинается с заголовка. Заголовок состоит из имени процедуры (его пользователь определяет сам), далее следует обязательный оператор присваивания := и служебное слово proc, после которого в круглых скобках через запятую указываются формальные параметры процедуры. Во избежание неполадок работы процедуры, рекомендуется в строке заголовка процедуры описывать переменные, которые будут использоваться только внутри тела процедуры (они называются локальными переменными). Для этого используется служебное слово local, после которого через запятую перечисляются локальные переменные. После заголовка следует основное тело процедуры, состоящее из составленных пользователем команд, причем последняя команда будет выводить окончательный результат выполнения процедуры. Процедура должна обязательно оканчиваться служебным словом end. Общий вид процедуры (стандартный синтаксис): > name:=proc(var1, var2, …) local vloc1, vloc2,…; > expr1; > expr2; …………… > exprn; > end; В Maple нет команды, позволяющей производить разложение функции в тригонометрический ряд Фурье. Однако можно создать собственную процедуру разложения ряд Фурье. Пусть требуется разложить на интервале [ x 1, x 2] 2 l -периодическую функцию f (x). Тогда ряд Фурье имеет вид:
где l =(x 2 x 1)/2;
Получить первые n членов ряда Фурье можно с помощью следующей процедуры: > fourierseries:=proc(f,x,x1,x2,n) local k, l, a, b, s; > l:=(x2-x1)/2; > a[0]:=int(f,x=x1..x2)/l; > a[k]:=int(f*cos(k*Pi*x/l),x=x1..x2)/l; > b[k]:=int(f*sin(k*Pi*x/l),x=x1..x2)/l; > s:=a[0]/2+sum(a[k]*cos(k*Pi*x/l)+ b[k]*sin(k*Pi*x/l), k=1..n); > end; Порядок обращения к этой процедуре такой: fourierseries(f,x,x1,x2,n), где f – имя функции, разложение которой требуется найти, где х – имя независимой переменной, где х1, x2 – интервал разложения, где n – число членов ряда.
|

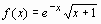 в окрестности х 0=0, удерживая 5 первых членов.
в окрестности х 0=0, удерживая 5 первых членов.
 и его разложения в ряд Тейлора в окрестности нуля.
и его разложения в ряд Тейлора в окрестности нуля.

 в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
в ряд Тейлора в окрестности точки (0, 0) до 6-ого порядка.
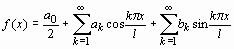 ,
, ;
;  ;
;  .
.


