Задание 4.1.
1. Найти полную и N -частичную суммы ряда, общий член которого равен: an = > restart: a[n]:=1/((3*n-2)*(3*n+1)); an:= > S[N]:=Sum(a[n], n=1..N)=sum(a[n], n=1..N);
> S:=limit(rhs(S[N]), N=+infinity);
2. К какой функции сходится степенной ряд: > Sum((-1)^(n+1)*n^2*x^n, n=1..infinity)= sum((-1)^(n+1)*n^2*x^n, n=1..infinity);
3. Найти сумму степенного ряда > Sum((1+x)^n/((n+1)*n!), n=0..infinity)= sum((1+x)^n/((n+1)*n!), n=0..infinity);
4. Найти сумму биномиального ряда > Sum(binomial(n,4)*(1-x)^n, n=1..infinity)= sum(binomial(n,4)*(1-x)^n, n=1..infinity);
5. Вычислить бесконечное произведение: > Product((n^3-1)/(n^3+1),n=2..infinity)= product((n^3-1)/(n^3+1), n=2..infinity);
Разложение функции в степенной ряд и ряд Тейлора. Разложение функции f (x) в степенной ряд в окрестности точки а
осуществляется командой series(f(x), x=a, n), где а – точка, в окрестности которой производится разложение, n – число членов ряда. Аналогичного действия команда taylor(f(x), x=a, n) раскладывает функции f(x) в окрестности точки x=a до порядка n -1 по формуле Тейлора. Команды series и taylor выдают результат, имеющий тип series. Для того, чтобы иметь возможность дальнейшей работы с полученным разложением, его следует преобразовать в полином с помощью команды convert(%,polynom). Функцию многих переменных f (x 1,…, xn) можно разложить в ряд Тейлора по набору переменных (x 1,…, xn) в окрестности точки (a 1,…, an) до порядка n с помощью команды mtaylor(f(x), [x1,…,xn], n). Эта команда находится в стандартной библиотеке, поэтому перед использованием должна быть вызвана readlib(mtaylor).
|

 .
.
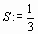
 ?
? .
. .
.
 .
.

 .
.



