Интегральные преобразования
В Maple имеется пакет inttrans, в котором содержатся команды различных интегральных преобразований.
Преобразование Фурье. Прямое преобразование Фурье функции f (x) вычисляется по формуле
В Maple оно может быть найдено командой fourier(f(x),x,k), где x переменная, по которой производится преобразование, k имя переменной, которое следует присвоить параметру преобразования. Обратное преобразование Фурье задается формулой
и вычисляется командой invfourier(F(k),k,x). Описанное выше прямое и обратное преобразования Фурье называются комплексными и применяются в тех случаях, когда функция f (x) задана на всей числовой оси. Если функция f (x) задана только при х >0, то рекомендуется использовать синус- и косинус- преобразования Фурье. Прямое и обратное синус-преобразования Фурье функции f (x) определяются формулами
Поскольку формулы синус-преобразования Фурье симметричны относительно замены x на k, то в Maple эти преобразования вычисляются одной командой, но с различным порядком указания параметров: fouriersin(f(x),x,k) вычисляет прямое синус-преобразование Фурье; fouriersin(F(k),k,x) вычисляет обратное синус-преобразование Фурье. Аналогично, прямое и обратное косинус-преобразования Фурье функции f (x) определяются формулами
В Maple эти преобразования вычисляются одной командой, но с различным порядком указания параметров: fourierсоs(f(x),x,k) вычисляет прямое косинус-преобразование Фурье; fourierсоs(F(k),k,x) вычисляет обратное косинус-преобразование Фурье.
|

 .
.
 и
и  .
.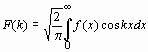 и
и  .
.


