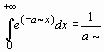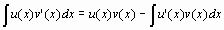Интегрирование
Аналитическое и численное интегрирование. Неопределенный интеграл 1. прямого исполнения – int(f, x), где f – подынтегральная функция, x – переменная интегрирования; 2. отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполнения int. Команда Int выдает на экран интеграл в аналитическом виде математической формулы. Для вычисления определенного интеграла > Int((1+cos(x))^2, x=0..Pi)= int((1+cos(x))^2, x=0..Pi);
Если в команде интегрирования добавить опцию continuous: int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity. Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число знаков после запятой).
Интегралы, зависящие от параметра. Ограничения для параметров. Если требуется вычислить интеграл, зависящий от параметра, то его значение может зависеть от знака этого параметра или каких-либо других ограничений. Рассмотрим в качестве примера интеграл > Int(exp(-a*x),x=0..+infinity)= int(exp(-a*x),x=0..+infinity); Definite integration: Can't determine if the integral is convergent. Need to know the sign of --> a Will now try indefinite integration and then take limits.
Таким способом интеграл с параметром не вычислить. Для получения явного аналитического результата вычислений следует сделать какие-либо предположения о значении параметров, то есть наложить на них ограничения. Это можно сделать при помощи команды assume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны. После наложения ограничений на параметр Maple добавляет к его имени символ (~), например параметр a, на который были наложены некоторые ограничения, в сроке вывода будет иметь вид: a ~. Описание наложенных ограничений параметра a можно вызвать командой about(a). Пример: наложить ограничения на параметр a такие, что a > - 1, a< 3: > assume(a>-1); additionally(a<=3); > about(a); Originally a, renamed a~: is assumed to be: RealRange(Open(-1),3) Вернемся к вычислению интеграла с параметром > assume(a>0); > Int(exp(-a*x),x=0..+infinity)= int(exp(-a*x),x=0..+infinity);
Обучение основным методам интегрирования. В Maple имеется пакет student, предназначенный для обучения математике. Он содержит набор подпрограмм, предназначенных для выполнения расчетов шаг за шагом, так, чтобы была понятна последовательность действий, приводящих к результату. К таким командам относятся интегрирование по частям inparts и замена переменной changevar. Формула интегрирования по частям:
Если обозначить подынтегральную функцию f=u (x) v’ (x), то параметры команды интегрирования по частям такие: intparts(Int(f, x), u),где u – именно та функция u(x), производную от которой предстоит вычислить по формуле интегрирования по частям. Если в интеграле требуется сделать замену переменных x=g (t) или t=h (x), то параметры команды замены переменных такие: changevar(h(x)=t, Int(f, x), t),где t ;новая переменная. Обе команды intparts и changevar не вычисляют окончательно интеграл, а лишь производят промежуточную выкладку. Для того, чтобы получить окончательный ответ, следует, после выполнения этих команд ввести команду value(%); где % - обозначают предыдущую строку. Не забудьте, перед использованием описанных здесь команд обязательно загрузить пакет student командой with(student).
|

 вычисляется с помощью 2-х команд:
вычисляется с помощью 2-х команд: в командах int и Int добавляются пределы интегрирования, например,
в командах int и Int добавляются пределы интегрирования, например,

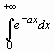 , который, как известно из математического анализа, сходится при а >0 и расходится при а <0. Если вычислить его сразу, то получится:
, который, как известно из математического анализа, сходится при а >0 и расходится при а <0. Если вычислить его сразу, то получится: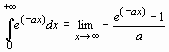 .
.