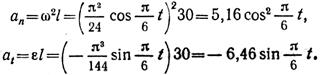Решение. Стер­жень OA совершает вращательное (коле­бательное) движение

 

Стер­жень OA совершает вращательное (коле­бательное) движение. Максимальные углы отклонения стержня от вертикали соот­ветствуют наиболь­шим абсолютным значениям функции sin (πt/6). Очевидно, это имеет место при sin (πt/6) = ± 1:

При t₁ = 3 с φ_тах = π;/4, при t₂ = 9 с φ_тах = -- π/4.

Крайние положения стержня OA на рис. 1.47 пока­заны штриховыми линиями OA₁ и ОА₂.

Напомним, что за положительное направление считаем вращение по часовой стрелке.

Уравнение изменения угловой скорости стержня OA

Уравнение изменения углового ускорения стержня OA

Направления ω; и ε; показаны на рис. 1.47. В приве­денном примере направления ω; и ε; противоположны. Следовательно, стержень OA совершает замедленное вра­щательное движение.

Нормальное и касательное ускорения шарика опреде­ляются по формулам:

В рассматриваемом примере касательное ускорение шари­ка направлено к точке С (рис. 1.47).

Определим момент времени, при котором а_п равно нулю. Для этого выражение а_п приравняем нулю:

Записанное условие выполняется при

но

Тогда

Нормальное ускорение шарика равно нулю, когда стержень OA занимает крайние положения.

Определим момент времени, при котором a_t равно нулю. Для этого выражение a_t приравняем нулю:

Это условие выполняется при

Касательное ускорение шарика обращается в ноль в тот момент, когда стержень OA совпадает с линией OC. Вычислим а_n и a_t при t = 1,5 с:

Ускорение шарика при t = 1,5 с

 

Угол между вектором ускорения шарика и стержнем OA определяется из соотношения

Откуда

 

Пример 11. Через 30 с равномерного вращательного движения с частотой n ₀ = 600 об/мин тело начало равнозамедленное движение и в течение последую­щих 20 с частота вращения тела уменьшилась до n = 450 об/мин.

Определить угловое ускорение тела при равнозамедленном вращательном движении, а также количество оборотов тела за время равномерного и равнозамедленного движения.