Соотношение между приведенной стоимостью акций и её номиналом в зависимости от ставки купонного дохода.
Рассчитать текущую стоимость облигаций номиналом в 5 тысяч у.е. Ставка купонного дохода 10%. Срок погашения 5 лет. Если ставка дисконта равна 1) =8%, 2) =10%, 3)=12%. Купонный доход начисляется один раз в год
Pvобл8%= Pvобл10%= Pvобл12%= Соотношение между текущей стоимостью облигаций и её номиналом зависит от соотношения ставки купонного дохода и ставки дисконта. Если ставка купонного дохода больше ставки дисконта, то текущая стоимость облигаций больше её номинала. Если ставка купонного дохода равна ставке дисконта, то текущая стоимость облигаций равна её номиналу. Если ставка купонного дохода меньше ставки дисконта, то текущая стоимость облигаций меньше её номинала. Выгодно покупать облигацию, если её текущая стоимость больше номинала. Инвестиции в облигации будут выгодными, если ставка купонного дохода больше минимальной доходности, которую требует инвестор. Рассмотрим задачу(выше) если доход начисляется 2 раза в год. Iэф=(1+0,1/2)^2 -1 = 0.1025 à Iэф=10,25%
I=0.1025*5000=512.5
Pобл10%= Если проценты начисляются чаще одного раза в год, то эффективная ставка превышает номинальную ставку купонного дохода, т.е 10,25%>10%, то в этом случае текущая стоимость облигаций больше её номинала и данные инвестиции в ценные бумаги становятся выгодными для инвесторов.
|

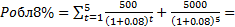 5351
5351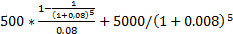 = 5351
= 5351 = 5000
= 5000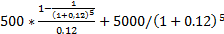 = 4639
= 4639 = 5047
= 5047


