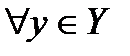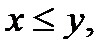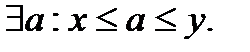Прямая на плоскости. Различные формы уравнений прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.
Вектор n, перпендикулярный прямой, называется вектором нормали, а вектор а, параллельный прямой, называется направляющим вектором данной прямой. 1. Уравнение прямой l, проходящей через данную точку М0 (х0,у0) и имеющей данную нормаль n(А,В): А*(х-х0)+В*(у-у0)=0. Это уравнение выражает условие перпендикулярности вектора М0М, где М произвольная точка прямой, и вектора нормали. 2. Общее уравнение прямой – это уравнение первой степени: Ах+Ву+С=0 Геометрический смысл коэффициентов при неизвестных в общем уравнении прямой: коэффициенты А и В в уравнении – это координаты вектора нормали n ┴ l. 3. Уравнение прямой, проходящей через данную точку М0 (х0,у0) и имеющей данный направляющий вектор а(а1,а2) (каноническое уравнение прямой): (х-х0)/а1=(у-у0)/а2. Это уравнение выражает условие параллельности вектора М0М, где М произвольная точка прямой, и направляющего вектора. 4. Уравнение прямой, проходящей через 2 данные точки М1(х1,у1) и М2(х2,у2): (х-х1)/(х2-х1)=(у-у1)/(у2-у1) 5. Уравнение прямой с угловым коэффициентом: l: y=kx+b 6. Уравнение прямой в отрезках: х/a+y/b=1 Угол между прямыми: Угол ᵠ= ﮮ (l1,l2) между двумя прямыми l 1: A1x+B1y+C1=0 и l 2:A2x+B2y+C2=0 равен углу между их нормалями и поэтому cosᵠ=(n1,n2)/│n1││n2│= (A1A2+B1B2)/ Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой. 1.8. Уравнение плоскости в пространстве. Угол между плоскостями. 1. Уравнение плоскости, проходящей через данную точку М0(x0,y0,z0) и имеющей данную нормаль n(A,B,C): А*(х-х0)+В*(у-у0)+С*(z-z0)=0 2. Общее уравнение плоскости: Ах+By+Cz+D=0 3. Уравнение плоскости, проходящей через данную точку М0(x0,y0,z0) параллельно двум данным векторам а(а1,а2,а3) и b(b1,b2,b3) – «направляющим векторам»:
Угол между двумя плоскостями (прямыми): Угол ᵠ= ﮮ (l1,l2) между двумя прямыми l 1: A1x+B1y+C1=0 и l 2:A2x+B2y+C2=0 равен углу между их нормалями и поэтому cosᵠ=(n1,n2)/│n1││n2│= (A1A2+B1B2)/
1.9. Уравнение прямой в пространстве. Угол между прямой и плоскостью и угол между прямыми в пространстве. А1х+В1у+С1z+D1=0 A2x+B2y+C2z+D2=0 – общие уравнения прямой в пространстве. Канонические уравнения прямой: (x-x0)/a1 = (y-y0)/a2=(z-z0)/a3 Параметрические уравнения прямой: X=x0+a1t, Y=y0+a2t, Z=z0+a3t. Угол между прямыми равен углу между их направляющими векторами. Угол ᵠ= ﮮ (l,П) между прямой l и плоскостью П – это один из смежных углов, образованных этой прямой и её проекцией на плоскость. Ясно, что один из этих углов равен ᵠ=П/2 - ﮮ(a,n) и поэтому sinᵠ=±cos(ﮮ(a,n))=±(a,n)/│a││n│ 1.10. Кривые второго порядка: эллипс, парабола, гипербола. Канонические уравнения. Приведение пятичленного уравнения к каноническому виду. Эллипсом называется геометрическое место точек М на плоскости, для которых сумма расстояний от двух фиксированных точек F1 и F2, называемых фокусами, есть величина постоянная и обозначаемая 2а. r1+r2=2a, где r1 и r2 – фокальные радиусы точки М. Каноническое уравнение эллипса: x^2/a^2+y^2/b^2=1, где b^2=a^2-c^2. Гиперболой называется геометрическое место точек М, для которых модуль разности расстояний от двух фиксированных точек F1 и F2, называемых фокусами, есть величина постоянная и обозначаемая 2а. r1 и r2 – фокальные радиусы точки М. Каноническое уравнение гиперболы: ^2/a^2-y^2/b^2=1, где b^2=c^2-a^2. Параболой называется геометрическое место точек М, для которых расстояние r до фиксированной точки F, называемой фокусом, равно расстоянию d до фиксированной прямой l, называемой директрисой. Каноническое уравнение параболы: y^2=2px, где р- расстояние от фокуса до директрисы (параметр). 2,1. Множество вещественных чисел. Функция. Область её определения Сложные и обратные функции. График функции. Из элементарной математики известно, что совокупность рациональных и иррациональных чисел образует множество действительных чисел R. На нем определены операции:1)Сложение: для любой пары действительных чисел а и b определено единственное число a+b, называемое их суммой, причем выполняются следующие условия: а) a+b=b+a; b) a+(b+c)=(a+b)+c; c) существует число 0 такое, что а+ 0 =а для любого а d) 2)Умножение: а) ab=ba b) a(bc)=(ab)c c) существует число 1 такое, что а· 1= а d) Множество действительных чисел обладает следующими свойствами:1)Упорядоченность - 2)Непрерывность – для любых непустых множеств Х и Y таких, что Если каждому элементу х множества Х (называемого областью определения функции) по определенному закону ставится в соответствие единственный элемент у множества Y, то подобное отображение называется функцией, определенной на множестве Х со значениями в множестве Y. При этом х называется независимой переменной, или аргументом, а у = f(x) – зависимой переменной, или функцией. Если у=F(u) является функцией от u, a u=φ(x) – функцией от х, то у = F [ φ(x)]называется сложной функцией или функцией от функции. Если для функции у = f(х) можно определить функцию х = g(у), ставящую в соответствие каждому значению функции у = f(x) значение ее аргумента х, то функция у = g(x) называется обратной функцией к у = f(x) и обозначается y = f –1(x).
|

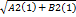 *
* 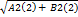
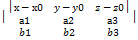 =0
=0 R
R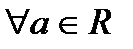
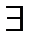 противоположное число –а, для которого а+(-а)= 0.
противоположное число –а, для которого а+(-а)= 0.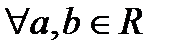 определено единственное число ab, называемое их произведением, такое, что выполняются следующие условия:
определено единственное число ab, называемое их произведением, такое, что выполняются следующие условия: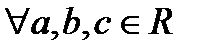
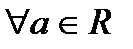
 a
a 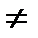 0 существует обратное число 1/ а, для которого а · 1/ а = 1.
0 существует обратное число 1/ а, для которого а · 1/ а = 1.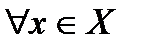 и
и