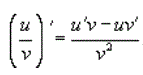Существование наибольшего и наименьшего значений непрерывной
функции на отрезке. Существование наибольшего и наименьшего значений функции следует из теоремы Вейерштрасса, в которой утверждается, что если функция непрерывна на отрезке, то функция принимает на нём наибольшее и наименьшее значения, то есть существуют точки отрезка, в которых функция принимает наибольшее и наименьшее на значения. Если при этом она имеет конечное число критических точек, то найти эти значения можно по следующему алгоритму: Найти D (f). Определить как непрерывную и дифференцируемую на своей области определения и на. Найти критические точки, выбрать те из них, которые принадлежат. Найти значения функции в этих критических точках и на концах отрезка. Максимальное из найденных чисел задаёт наибольшее значение функции на отрезке, а минимальное соответственно наименьшее. 2,9. Теорема о промежуточных значениях функции непрерывной на отрезке. Если функция у(х) непрерывна на отрезке [a,b] и у(a) =/= у(b), то для любого числа М между у(a) и у(b) найдется внутри (a,b) хотя бы одна точка х0 такая, что у(х0)=М. Доказательство опирается на теорему Коши: Если у(a)*у(b) < 0, то внутри (a,b) найдется хотя бы одна точка х0 такая, что у(х0)=0. Достаточно рассмотреть функцию у(х)-М и сослаться на теорему Коши. А вот док-во теоремы Коши не такое короткое, хотя утверждение геометрически совершенно очевидно. Теорема Коши (о промежуточных значениях непрерывной функции) пусть функция f(x) непрерывна на отрезке [a,b] и на концах этого отрезка принимает значения разных знаков, тогда найдется такая точка, в которой значение функции равно нулю. 3,1. Определение производной, её геометрический и механический смысл. Производной функции y=f(x) в точке х нулевое,называется предел отношения приращения функции к приращению аргумента,когда приращение аргумента стремится к нулю. Если существует конечный предел f в точке х0. Обозначение: Разность Геометрический смысл:значение производной при данном значении х равно тангенсу угла, образованного касательной к графику функции в точке с соответствующим значением х с положительным направлением оси Ох. Механический смысл производной. Рассмотрим прямолинейное движение тела, для которого пройденное расстояние есть функция от времени: s=f(t). Среднюю скорость за время Δ;t можно определить по формуле:
3,2. Производная суммы, произведения и частного. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций: Производная произведения функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и
Производная частного функций. Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле
|

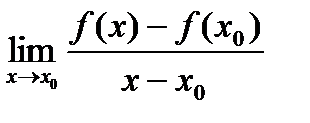 , то он называется производной функции
, то он называется производной функции
 называется приращением аргумента, а
называется приращением аргумента, а  - приращением функции. Таким образом, можно определить производную как
- приращением функции. Таким образом, можно определить производную как  .
. . Для определения мгновенной скорости тела в данный момент времени устремим Δ;t к нулю. Получим:
. Для определения мгновенной скорости тела в данный момент времени устремим Δ;t к нулю. Получим:  Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответственно производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом х .
Таким образом, производная от расстояния в данный момент времени равна мгновенной скорости движения в этот момент. Соответственно производная любой функции при данном значении аргумента равна скорости изменения этой функции при рассматриваемом х .
 Производная произведения двух функций не равана произведению производных этих функций.
Производная произведения двух функций не равана произведению производных этих функций.