Элементарных функций по формуле Тейлора. Применение формулы
Тейлора для приближённых вычислений. Производные порядка выше первого называются производными высших порядков. Производная у'=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка. Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у" Итак, у"=(у')'. Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)). Итак, у'"=(y")' Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:y(n)=(y(n-1))¢ Свойства производных высших порядков. Основные свойства производных высших порядков следуют из соответствующих свойств первой производной: 1.(cf(x))(n)=c·f(n)(x). 2.(f(x)+g(x))(n)=f(n)(x)+g(n)(x). 3.Для y=xm y(n)=n(n-1)…(n-m+1)xm-n. Если m – натуральное число, то при n>m y(n)=0. 4.Можно вывести так называемую формулу Лейбница, позволяющую найти производную n-го порядка от произведения функций f(x)g(x) Формула Тейлора: Если функция y=f(x)имеет (n+1)-ю производную в окрестности точки
Если (n+1)-я производная Действительно, Применение формулы Тейлора для приближенных вычислений. Заменяя какую-либо функцию, для которой известно разложение по формуле Тейлора, многочленом Тейлора, степень которого выбирается так, чтобы величина остаточного члена не превысила выбранное значение погрешности, можно находить приближенные значения функции с заданной точностью. Найдем приближенное значение числа е, вычислив значение многочлена Тейлора
|

 .
.
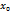 ,то остаточный член
,то остаточный член  (x) можно представить в форме Лагранжа:
(x) можно представить в форме Лагранжа:  , где с-некоторая внутренняя точка отрезка [
, где с-некоторая внутренняя точка отрезка [ 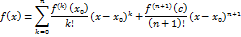
 ограничена в окрестности точки
ограничена в окрестности точки  ,например если она непрерывна,то остаточный член можно представить в форме Пеано:
,например если она непрерывна,то остаточный член можно представить в форме Пеано:  ,
, . Получаем формулу Тейлора с остаточным членом в форме Пеано:
. Получаем формулу Тейлора с остаточным членом в форме Пеано:  .
. при n=8:
при n=8:  При этом
При этом 



