Предел функции. Свойства функции имеющих предел. Односторонние
пределы. Пределы монотонных функций. Число А называется пределом функции у = f(x) при х, стремящемся к х 0, если Обозначение: Свойства пределов:1).Если существует Доказательство. Так как для любого ε существует такое δ, что | f(x) - A | < ε при | x - x0 | < δ, то при этом | f(x)| < |A | + ε, то есть функция ограничена в рассматриваемой окрестности. 2). Функция не может иметь двух различных пределов при х, стремящемуся к одному и тому же значению. Доказательство. Пусть А и В – пределы f(x) при х→х0. Выберем ε < | A-B |. Тогда существует такое δ1, что | f(x)-A |<ε/2 при | x - x0 | < δ1, и такое δ2, что |f (x)-B |<ε/2 при | x - x0 | < δ2. Если выбрать в качестве δ меньшее из чисел δ1 и δ2, то значения функции f(x) для аргументов, лежащих в δ – окрестности х 0, должны одновременно находиться в двух непересекающихся окрестностях, что невозможно. Утверждение доказано. 3)Если Доказательство. Достаточно выбрать ε=| A |/2. Тогда для х из некоторой окрестности х 0 | f(x)-A | < | A |/2, то есть А /2 < f(x) <;3 A /2 при A > 0 и 3 A /2 < f(x) < A /2 при A < 0. Следовательно, в выбранной окрестности f(x) сохраняет постоянный знак. Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.
Если Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю то функция называется стро́го моното́нной.
Если Если Класс функций
|

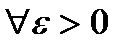
 такое, что | f(x) - A | < ε при | x - x0 | < δ.
такое, что | f(x) - A | < ε при | x - x0 | < δ. .
. , то существует окрестность точки х 0, в которой функция f(x) сохраняет постоянный знак (f(x)>;0, если A > 0, и f(x)<0, если A < 0).
, то существует окрестность точки х 0, в которой функция f(x) сохраняет постоянный знак (f(x)>;0, если A > 0, и f(x)<0, если A < 0). — правосторонний предел, если
— правосторонний предел, если 
 — левосторонний предел, если
— левосторонний предел, если 
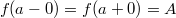 ,то
,то 

 , то
, то  возрастает, пишут
возрастает, пишут  .
.



