Производная по направлению. Градиент. Касательная плоскость и
нормаль к поверхности. Геометрический смысл ЧП-ой состоит в следующем: значение ЧП-ой по переменной «х» = тангенсу угла наклона на касательной проведённой к кривой получаемой пересечением поверхностей Z=f(x,y) и плоскости у=у0.Анологично опр-ся геометрический смысл ЧП-ой по переменной «у». Значение ЧП-ой по переменной «у» = тангенсу угла наклона касательной проведённой к кривой к-рая получается при пересечении поверхности с плоскостью х=х0 Геометрический смысл дифференциала: Если к графику гладкой функции в некоторой точке построить касательную, то, отложив на касательной такой отрезок, чтобы его проекция на ось Ох равнялась дельтаХ, получим в проекции на ось Оу отрезок, равный дифференциалу функции в точке касания. Производной функции u=u(P)=u(x,y,z) по направлению l(или по направлению вектора е)в точке Градиентом функции u=u(x,y,z)называется векторное поле,координатами которого являются частные производные функции u: Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке. Из этого определения следует, что уравнение касательной плоскости имеет вид: F'x (x0, y0, z0) · (x − x0) + F'y (x0, y0, z0) · (y − y0) + F'z (x0, y0, z0) · (z − z0) = 0. Если точка поверхности является особой, то в этой точке нормальный к поверхности вектор может не существовать, и, следовательно, поверхность может не иметь нормали и касательной плоскости. Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку. 4,5. Неявные функции. Дифференцирование неявных функций. Неявной функцией от переменных x,y называется соответствие, которое определяется уравнением F(x,y,z)=0,где F(x,y,z)-некоторая функция трех переменных. Если неявная функция задана уравнением F(x; у)=0, то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по x, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у'. Производная неявной функции выражается через аргумент х и функцию у. Пример: Найти производную функции у, заданную уравнением х3+у3-3ху=0. Решение: Функция у задана неявно. Дифференцируем по х равенство х3+у3-3ху=0. Из полученного соотношения 3х2+3у2· у'-3(1· у+х· у')=0 следует, что у2у'-ху'=у-х2, т. е. у'=(у-х2)/(у2-х). 4,6. Частные производные высших порядков. Частные производные порядка n функции z=f(x,y)получаются в результате n последовательных дифференцирований этой функции. Если получающиеся при этом смешанные производные непрерывны,то по теореме(Теорема:Если функция z=f(x,y)имеет смешанные производные
|

 называется предел отношения приращения функции в направлении l к «приращению аргумента»:
называется предел отношения приращения функции в направлении l к «приращению аргумента»: 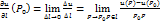 . В частности,если l совпадает с одной из осей координат,мы получаем определение частной производной.
. В частности,если l совпадает с одной из осей координат,мы получаем определение частной производной. .
. и
и  в некоторой окрестности точки
в некоторой окрестности точки  ,которые непрерывны в самой этой точке, то эти производные в точке
,которые непрерывны в самой этой точке, то эти производные в точке  равны:
равны:  ,т.е. производные не зависят от порядка дифференцирования.)они не зависят от порядка дифференцирований.
,т.е. производные не зависят от порядка дифференцирования.)они не зависят от порядка дифференцирований.


