Экстремума. Достаточное условие экстремума. Точка  называется точкой локального максимума (соответственно локального минимума)функции z=f(x,y),если f(
называется точкой локального максимума (соответственно локального минимума)функции z=f(x,y),если f( )
)  f(M) (соответственно f(
f(M) (соответственно f( )
)  f(M)) для M(x,y) в некоторой окрестности точки
f(M)) для M(x,y) в некоторой окрестности точки  . Точки локального максимума и локального минимума называются точками локального экстремума.
. Точки локального максимума и локального минимума называются точками локального экстремума.
Необходимое условие: Если  -точка локального экстремума функции z=f(M)=f(
-точка локального экстремума функции z=f(M)=f( )и в этой точке существуют частные производные,то эти производные равны нулю:
)и в этой точке существуют частные производные,то эти производные равны нулю:  i=1,…,n.Точка
i=1,…,n.Точка  называется критической (или стационарной)точкой функции z=f(M),если в этой точке существуют частные производные и все они обращаются в нуль:
называется критической (или стационарной)точкой функции z=f(M),если в этой точке существуют частные производные и все они обращаются в нуль:  при I=1,…,n. Критические точки функции z=f(x,y) находятся из системы:
при I=1,…,n. Критические точки функции z=f(x,y) находятся из системы:  .
.
Достаточные условия: Пусть функция z=f(x,y) имеет непрерывные частные производные второго порядка в окрестности точки  и пусть
и пусть 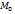 есть критическая точка,т.е.
есть критическая точка,т.е. 
 . Тогда
. Тогда
1)если H( )>0,то
)>0,то  -точка локального экстремума,причем
-точка локального экстремума,причем
1+)если 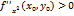 ,то
,то  - точка локального минимума;
- точка локального минимума;
1-)а если  ,то
,то  - точка локального максимума;
- точка локального максимума;
2)если H( )<0,то
)<0,то  не является точкой локального экстремума (а является седловой точкой);
не является точкой локального экстремума (а является седловой точкой);
3)если H( ) =0,то экстремум в точке
) =0,то экстремум в точке  может быть, а может не быть и для исследования нужно привлекать производные третьего порядка.
может быть, а может не быть и для исследования нужно привлекать производные третьего порядка.

 называется точкой локального максимума (соответственно локального минимума)функции z=f(x,y),если f(
называется точкой локального максимума (соответственно локального минимума)функции z=f(x,y),если f( )
)  f(M) (соответственно f(
f(M) (соответственно f( f(M)) для M(x,y) в некоторой окрестности точки
f(M)) для M(x,y) в некоторой окрестности точки  -точка локального экстремума функции z=f(M)=f(
-точка локального экстремума функции z=f(M)=f( )и в этой точке существуют частные производные,то эти производные равны нулю:
)и в этой точке существуют частные производные,то эти производные равны нулю:  i=1,…,n.Точка
i=1,…,n.Точка  при I=1,…,n. Критические точки функции z=f(x,y) находятся из системы:
при I=1,…,n. Критические точки функции z=f(x,y) находятся из системы:  .
.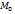 есть критическая точка,т.е.
есть критическая точка,т.е. 
 . Тогда
. Тогда )>0,то
)>0,то 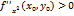 ,то
,то  ,то
,то  - точка локального максимума;
- точка локального максимума;


