Прогрессии. Арифметическая и геометрическая прогрессии.
Арифметическая прогрессия — числовая последовательность вида
то есть последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
Арифметическая прогрессия является монотонной последовательностью. При · Натуральный ряд · · Если все элементы некоторой последовательности равны между собой и равны некоторому числу · Сумма первых
Геометрическая прогрессия — последовательность чисел
|
,
(шага или разности прогрессии):
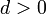она является возрастающей, а при 
— убывающей. Если 
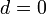, то последовательность будет стационарной. Эти утверждения следуют из соотношения 
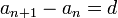для членов арифметической прогрессии.
— это арифметическая прогрессия, в которой первый член 
, а разность 
.
— первые 5 членов арифметической прогрессии, в которой 
.
, то это есть арифметическая прогрессия, в которой 
и 
есть арифметическая прогрессия с разностью 
натуральных чисел выражается формулой
.
(членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число 
(знаменатель прогрессии), где 
, 
: 
.
