Простейшие элементарные функции и их графики (постоянная и степенная).
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
· алгебраические:
· степенная;
· рациональная.
· трансцендентные:
· показательная и логарифмическая;
· тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
Постоянной называется функция, заданная формулой у = b, где b - некоторое число.
Графиком постоянной функции у = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. На рисунке изображены графики нескольких постоянных функций. В частности, графиком функции y = 0 является ось абсцисс.
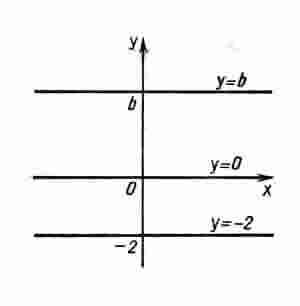
Если b = 0, то получаем прямую пропорциональность у = kх.
Функция у = хn, где n - натуральное число, называется степенной функцией с натуральным показателем. При n = 1 получаем функцию у = х. При n = 2 получаем функцию у = х2.
Функция у = х2.
Перечислим свойства функции у = х2. 1) Область определения функции - вся числовая прямая. 2) у = х2 - четная функция (f (- х) = (- х)2 = х2 = f (x)). 3) На промежутке [0; + ∞) функция возрастает (если 0 ≤ х1 < х2, то х12 < х22, а это и означает возрастание функции). 4) На промежутке (- ∞; 0] функция убывает (если x1 < x2 ≤ 0, то х12 > х22, а это и означает убывание функции).
Графиком функции у = х2 является парабола (см. рис).
 При n = 3 получаем функцию у = х3.
Функция у = х3.
Перечислим свойства функции у = х3. 1) Область определения функции - вся числовая прямая. 2) у = х3 - нечетная функция (f (- х) = (- х)3= - х3 = - f (x)) 3) Функция у = х3 возрастает на всей числовой прямой. График функции у = х3 изображен на рисунке. Он называется кубической параболой.
При n = 3 получаем функцию у = х3.
Функция у = х3.
Перечислим свойства функции у = х3. 1) Область определения функции - вся числовая прямая. 2) у = х3 - нечетная функция (f (- х) = (- х)3= - х3 = - f (x)) 3) Функция у = х3 возрастает на всей числовой прямой. График функции у = х3 изображен на рисунке. Он называется кубической параболой.
 Пусть n - произвольное четное натуральное число, большее двух: n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |x| > 1 тем круче идут вверх, чем больше n, а при |x| < 1 тем "теснее прижимаются" к оси х, чем больше n. (рис. а)
Пусть n - произвольное четное натуральное число, большее двух: n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |x| > 1 тем круче идут вверх, чем больше n, а при |x| < 1 тем "теснее прижимаются" к оси х, чем больше n. (рис. а)
 Пусть n - произвольное нечетное число, большее трех: n = 5, 7, 9, …. В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n) (рис. б). Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n.
Степенная функция с целым отрицательным показателем.
Рассмотрим функцию у = х -n, где n - натуральное число. При n = 1 получаем у = х -1 или у = 1/х. Свойства этой функции рассмотрены выше.
Пусть n - нечетное число, большее единицы, n = 3, 5, 7, … В этом случае функция у = х -n обладает в основном теми же свойствами, что и функция у = 1/х. График функции у = х -n (n = 3, 5, 7, …) напоминает график функции у = 1/х (рис. а).
Пусть n - произвольное нечетное число, большее трех: n = 5, 7, 9, …. В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n) (рис. б). Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n.
Степенная функция с целым отрицательным показателем.
Рассмотрим функцию у = х -n, где n - натуральное число. При n = 1 получаем у = х -1 или у = 1/х. Свойства этой функции рассмотрены выше.
Пусть n - нечетное число, большее единицы, n = 3, 5, 7, … В этом случае функция у = х -n обладает в основном теми же свойствами, что и функция у = 1/х. График функции у = х -n (n = 3, 5, 7, …) напоминает график функции у = 1/х (рис. а).
 Пусть n - четное число, например n = 2. Перечислим некоторые свойства функции у = х -2, т. е. функции у = 1/х2. 1) Функция определена при всех x ≠ 0 2) y =1/х2 - четная функция. 3) y = 1/х2 убывает на (0; + ∞) и возрастает на (- ∞; 0).
Теми же свойствами обладают любые функции вида у = х -n при четном n, большем двух.
График функции у = 1/х2 изображен на рисунке б. Аналогичный вид имеет график функции у = х -n, если n = 4, 6,...
Функция у = х1/2.
Перечислим свойства функции у =
Пусть n - четное число, например n = 2. Перечислим некоторые свойства функции у = х -2, т. е. функции у = 1/х2. 1) Функция определена при всех x ≠ 0 2) y =1/х2 - четная функция. 3) y = 1/х2 убывает на (0; + ∞) и возрастает на (- ∞; 0).
Теми же свойствами обладают любые функции вида у = х -n при четном n, большем двух.
График функции у = 1/х2 изображен на рисунке б. Аналогичный вид имеет график функции у = х -n, если n = 4, 6,...
Функция у = х1/2.
Перечислим свойства функции у =  . 1) Область определения - луч [0; + ∞). Это следует из того, что выражение . 1) Область определения - луч [0; + ∞). Это следует из того, что выражение  определено лишь при х ≥ 0. 2) Функция у = определено лишь при х ≥ 0. 2) Функция у =  ни четна, ни нечетна. 3) Функция у = ни четна, ни нечетна. 3) Функция у =  возрастает на луче [0; + ∞). График функции у = возрастает на луче [0; + ∞). График функции у =  изображен на рисунке а.. изображен на рисунке а..
 Функция у = х1/3.
Перечислим свойства функции у =
Функция у = х1/3.
Перечислим свойства функции у =  . 1) Область определения функции - вся числовая прямая. 2) Функция у = . 1) Область определения функции - вся числовая прямая. 2) Функция у =  нечетна. 3) Функция у = нечетна. 3) Функция у =  возрастает на всей числовой прямой. График функции у = возрастает на всей числовой прямой. График функции у =  изображен на рисунке б.
Функция у = х1/n.
При четном n функция y = изображен на рисунке б.
Функция у = х1/n.
При четном n функция y =  обладает теми же свойствами, что и функция у = обладает теми же свойствами, что и функция у =  , и график ее напоминает график функции у = , и график ее напоминает график функции у =  . При нечетном n функция у = . При нечетном n функция у =  обладает теми же свойствами, что и функция у = обладает теми же свойствами, что и функция у =  , и график ее напоминает график функции у = , и график ее напоминает график функции у =  . .
 Степенная функция с положительным дробным показателем.
Рассмотрим функцию у = хr, где r - положительная несократимая дробь. Перечислим некоторые свойства этой функции. 1) Область определения - луч [0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = хr возрастает на [0; + ∞).
На рисунке а изображен график функции у = х2,5.
Степенная функция с положительным дробным показателем.
Рассмотрим функцию у = хr, где r - положительная несократимая дробь. Перечислим некоторые свойства этой функции. 1) Область определения - луч [0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = хr возрастает на [0; + ∞).
На рисунке а изображен график функции у = х2,5.
 Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + ∞). Подобный вид имеет график любой функции вида у = хr, где r > 1. На рисунке б изображен график функции у = х2/3. Подобный вид имеет график любой степенной функции у = хr, где 0 < r < 1.
Степенная функция с отрицательным дробным показателем.
Рассмотрим функцию у = х -r, где r - положительная несократимая дробь.
Перечислим свойства этой функции. 1) Область определения - промежуток (0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = х -r убывает на (0; + ∞)
Построим график функции у = х -1/2 (рис. в). Подобный вид имеет график любой функции у = хr, где r - отрицательная дробь.
Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + ∞). Подобный вид имеет график любой функции вида у = хr, где r > 1. На рисунке б изображен график функции у = х2/3. Подобный вид имеет график любой степенной функции у = хr, где 0 < r < 1.
Степенная функция с отрицательным дробным показателем.
Рассмотрим функцию у = х -r, где r - положительная несократимая дробь.
Перечислим свойства этой функции. 1) Область определения - промежуток (0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = х -r убывает на (0; + ∞)
Построим график функции у = х -1/2 (рис. в). Подобный вид имеет график любой функции у = хr, где r - отрицательная дробь.
| | | |

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Машины и механизмы для нарезки овощей В зависимости от назначения овощерезательные машины подразделяются на две группы: машины для нарезки сырых и вареных овощей...
Классификация и основные элементы конструкций теплового оборудования Многообразие способов тепловой обработки продуктов предопределяет широкую номенклатуру тепловых аппаратов...
Именные части речи, их общие и отличительные признаки Именные части речи в русском языке — это имя существительное, имя прилагательное, имя числительное, местоимение...
|
Классификация холодных блюд и закусок. Урок №2 Тема: Холодные блюда и закуски. Значение холодных блюд и закусок. Классификация холодных блюд и закусок. Кулинарная обработка продуктов...
ТЕРМОДИНАМИКА БИОЛОГИЧЕСКИХ СИСТЕМ. 1. Особенности термодинамического метода изучения биологических систем. Основные понятия термодинамики. Термодинамикой называется раздел физики...
Травматическая окклюзия и ее клинические признаки При пародонтите и парадонтозе резистентность тканей пародонта падает...
|
|

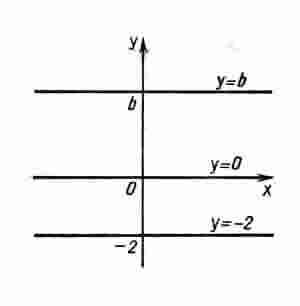
 При n = 3 получаем функцию у = х3.
Функция у = х3.
Перечислим свойства функции у = х3. 1) Область определения функции - вся числовая прямая. 2) у = х3 - нечетная функция (f (- х) = (- х)3= - х3 = - f (x)) 3) Функция у = х3 возрастает на всей числовой прямой. График функции у = х3 изображен на рисунке. Он называется кубической параболой.
При n = 3 получаем функцию у = х3.
Функция у = х3.
Перечислим свойства функции у = х3. 1) Область определения функции - вся числовая прямая. 2) у = х3 - нечетная функция (f (- х) = (- х)3= - х3 = - f (x)) 3) Функция у = х3 возрастает на всей числовой прямой. График функции у = х3 изображен на рисунке. Он называется кубической параболой.
 Пусть n - произвольное четное натуральное число, большее двух: n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |x| > 1 тем круче идут вверх, чем больше n, а при |x| < 1 тем "теснее прижимаются" к оси х, чем больше n. (рис. а)
Пусть n - произвольное четное натуральное число, большее двух: n = 4, 6, 8,.... В этом случае функция у = хn обладает теми же свойствами, что и функция у = х2. График такой функции напоминает параболу у = х2, только ветви графика при |x| > 1 тем круче идут вверх, чем больше n, а при |x| < 1 тем "теснее прижимаются" к оси х, чем больше n. (рис. а)
 Пусть n - произвольное нечетное число, большее трех: n = 5, 7, 9, …. В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n) (рис. б). Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n.
Степенная функция с целым отрицательным показателем.
Рассмотрим функцию у = х -n, где n - натуральное число. При n = 1 получаем у = х -1 или у = 1/х. Свойства этой функции рассмотрены выше.
Пусть n - нечетное число, большее единицы, n = 3, 5, 7, … В этом случае функция у = х -n обладает в основном теми же свойствами, что и функция у = 1/х. График функции у = х -n (n = 3, 5, 7, …) напоминает график функции у = 1/х (рис. а).
Пусть n - произвольное нечетное число, большее трех: n = 5, 7, 9, …. В этом случае функция у = хn обладает теми же свойствами, что и функция у = х3. График такой функции напоминает кубическую параболу (только ветви графика тем круче идут вверх, вниз, чем больше n) (рис. б). Отметим также, что на промежутке (0; 1) график степенной функции у = хn тем медленнее отдаляется от оси х с ростом х, чем больше n.
Степенная функция с целым отрицательным показателем.
Рассмотрим функцию у = х -n, где n - натуральное число. При n = 1 получаем у = х -1 или у = 1/х. Свойства этой функции рассмотрены выше.
Пусть n - нечетное число, большее единицы, n = 3, 5, 7, … В этом случае функция у = х -n обладает в основном теми же свойствами, что и функция у = 1/х. График функции у = х -n (n = 3, 5, 7, …) напоминает график функции у = 1/х (рис. а).
 Пусть n - четное число, например n = 2. Перечислим некоторые свойства функции у = х -2, т. е. функции у = 1/х2. 1) Функция определена при всех x ≠ 0 2) y =1/х2 - четная функция. 3) y = 1/х2 убывает на (0; + ∞) и возрастает на (- ∞; 0).
Теми же свойствами обладают любые функции вида у = х -n при четном n, большем двух.
График функции у = 1/х2 изображен на рисунке б. Аналогичный вид имеет график функции у = х -n, если n = 4, 6,...
Функция у = х1/2.
Перечислим свойства функции у =
Пусть n - четное число, например n = 2. Перечислим некоторые свойства функции у = х -2, т. е. функции у = 1/х2. 1) Функция определена при всех x ≠ 0 2) y =1/х2 - четная функция. 3) y = 1/х2 убывает на (0; + ∞) и возрастает на (- ∞; 0).
Теми же свойствами обладают любые функции вида у = х -n при четном n, большем двух.
График функции у = 1/х2 изображен на рисунке б. Аналогичный вид имеет график функции у = х -n, если n = 4, 6,...
Функция у = х1/2.
Перечислим свойства функции у =  . 1) Область определения - луч [0; + ∞). Это следует из того, что выражение
. 1) Область определения - луч [0; + ∞). Это следует из того, что выражение  Функция у = х1/3.
Перечислим свойства функции у =
Функция у = х1/3.
Перечислим свойства функции у =  . 1) Область определения функции - вся числовая прямая. 2) Функция у =
. 1) Область определения функции - вся числовая прямая. 2) Функция у =  обладает теми же свойствами, что и функция у =
обладает теми же свойствами, что и функция у =  Степенная функция с положительным дробным показателем.
Рассмотрим функцию у = хr, где r - положительная несократимая дробь. Перечислим некоторые свойства этой функции. 1) Область определения - луч [0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = хr возрастает на [0; + ∞).
На рисунке а изображен график функции у = х2,5.
Степенная функция с положительным дробным показателем.
Рассмотрим функцию у = хr, где r - положительная несократимая дробь. Перечислим некоторые свойства этой функции. 1) Область определения - луч [0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = хr возрастает на [0; + ∞).
На рисунке а изображен график функции у = х2,5.
 Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + ∞). Подобный вид имеет график любой функции вида у = хr, где r > 1. На рисунке б изображен график функции у = х2/3. Подобный вид имеет график любой степенной функции у = хr, где 0 < r < 1.
Степенная функция с отрицательным дробным показателем.
Рассмотрим функцию у = х -r, где r - положительная несократимая дробь.
Перечислим свойства этой функции. 1) Область определения - промежуток (0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = х -r убывает на (0; + ∞)
Построим график функции у = х -1/2 (рис. в). Подобный вид имеет график любой функции у = хr, где r - отрицательная дробь.
Он заключен между графиками функций у = х2 и у = х3, заданных на промежутке [0; + ∞). Подобный вид имеет график любой функции вида у = хr, где r > 1. На рисунке б изображен график функции у = х2/3. Подобный вид имеет график любой степенной функции у = хr, где 0 < r < 1.
Степенная функция с отрицательным дробным показателем.
Рассмотрим функцию у = х -r, где r - положительная несократимая дробь.
Перечислим свойства этой функции. 1) Область определения - промежуток (0; + ∞). 2) Функция ни четная, ни нечетная. 3) Функция у = х -r убывает на (0; + ∞)
Построим график функции у = х -1/2 (рис. в). Подобный вид имеет график любой функции у = хr, где r - отрицательная дробь.



