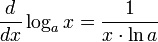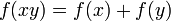Если рассматривать логарифмируемое число как переменную, мы получим логарифмическую функцию 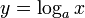 . Она определена при
. Она определена при 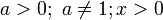 . Область значений:
. Область значений:  . Эта кривая часто называется логарифмикой [9]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси
. Эта кривая часто называется логарифмикой [9]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси  ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.
; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.
Из определения следует, что логарифмическая зависимость есть обратная функция для показательной функции 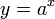 , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (cм. рисунок). Как и показательная, логарифмическая функция относится к категории трансцендентных функций.
, поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (cм. рисунок). Как и показательная, логарифмическая функция относится к категории трансцендентных функций.
Функция является строго возрастающей при  (см. далее графики) и строго убывающей при
(см. далее графики) и строго убывающей при  . График любой логарифмической функции проходит через точку
. График любой логарифмической функции проходит через точку  . Функция непрерывна и неограниченно дифференцируемавсюду в своей области определения.
. Функция непрерывна и неограниченно дифференцируемавсюду в своей области определения.
Ось ординат  является левой вертикальной асимптотой, поскольку:
является левой вертикальной асимптотой, поскольку:
 при
при 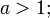
 при
при  .
.
Производная логарифмической функции равна:
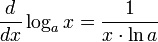
С точки зрения алгебры, логарифмическая функция осуществляет (единственно возможный) изоморфизм мультипликативной группы положительных вещественных чисел и аддитивной группы всех вещественных чисел. Другими словами, логарифмическая функция есть единственное (определённое для всех положительных значений аргумента) непрерывное решение функционального уравнения[10]:
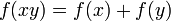

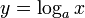 . Она определена при
. Она определена при 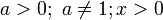 . Область значений:
. Область значений:  . Эта кривая часто называется логарифмикой [9]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси
. Эта кривая часто называется логарифмикой [9]. Из формулы замены основания логарифма видно, что графики логарифмических функций с разными основаниями, бо́льшими единицы, отличаются один от другого только масштабом по оси  ; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.
; графики для оснований, меньших единицы, являются их зеркальным отражением относительно горизонтальной оси.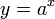 , поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (cм. рисунок). Как и показательная, логарифмическая функция относится к категории трансцендентных функций.
, поэтому их графики симметричны относительно биссектрисы первого и третьего квадрантов (cм. рисунок). Как и показательная, логарифмическая функция относится к категории трансцендентных функций. (см. далее графики) и строго убывающей при
(см. далее графики) и строго убывающей при  . График любой логарифмической функции проходит через точку
. График любой логарифмической функции проходит через точку  . Функция непрерывна и неограниченно дифференцируемавсюду в своей области определения.
. Функция непрерывна и неограниченно дифференцируемавсюду в своей области определения. является левой вертикальной асимптотой, поскольку:
является левой вертикальной асимптотой, поскольку: при
при 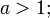
 при
при  .
.