Свойства пустого множества
· Ни одно множество не является элементом пустого множества. Иначе говоря, · Пустое множество является подмножеством любого множества. Иначе говоря, · Объединение пустого множества с любым множеством равно последнему [указанному множеству]. Иначе говоря, · Пересечение пустого множества с любым множеством равно пустому множеству. Иначе говоря, · Исключение пустого множества из любого множества равно последнему [указанному множеству]. Иначе говоря, · Исключение любого множества из пустого множества равно пустому множеству. Иначе говоря, · Симметрическая разность пустого множества с любым множеством равна последнему [указанному множеству]. Иначе говоря, · Декартово произведение пустого множества на любое множество равно пустому множеству. Иначе говоря, · Пустое множество — транзитивно. Иначе говоря, · Пустое множество — ординал. Иначе говоря, · Мощность пустого множества равна нулю. Иначе говоря, · Мера пустого множества равна нулю. Иначе говоря, Континуум (от лат. continuum — непрерывное) — мощность (или кардинальное число) множества всех вещественных чисел. Обозначается строчной латинской буквой c во фрактурном начертании: Также термин континуум может обозначать само множество вещественных чисел, или даже любое континуальное множество.
|

 и, в частности,
и, в частности,  .
.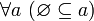 и, в частности,
и, в частности, 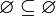 .
. и, в частности,
и, в частности,  .
.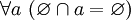 и, в частности,
и, в частности,  .
. и, в частности,
и, в частности,  .
. и, в частности,
и, в частности,  и, в частности,
и, в частности, 
 и, в частности,
и, в частности,  .
. , где
, где  .
.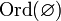 , где
, где  .
. .
.
 . Множество, имеющее мощность континуум, называется континуальным множеством.
. Множество, имеющее мощность континуум, называется континуальным множеством.


