Комплексные числа — расширение поля вещественных чисел, обычно обозначается  . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 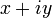 , где
, где  и
и  — вещественные числа,
— вещественные числа,  — мнимая единица.
— мнимая единица.
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени  с комплексными коэффициентами имеет ровно
с комплексными коэффициентами имеет ровно  комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
Если комплексное число  , то число
, то число  называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к  (обозначается также
(обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
·  (сопряжённое к сопряжённому есть исходное).
(сопряжённое к сопряжённому есть исходное).
· 
· 
· 
· 
Обобщение:  , где
, где  — произвольный многочлен с вещественными коэффициентами.
— произвольный многочлен с вещественными коэффициентами.
· 
· 
Значимость сопряжения объясняется тем, что оно является образующей группы Галуа  .
.

 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма 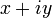 , где
, где  и
и  — вещественные числа,
— вещественные числа,  — мнимая единица.
— мнимая единица. с комплексными коэффициентами имеет ровно
с комплексными коэффициентами имеет ровно  , то число
, то число  называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к  (обозначается также
(обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком. (сопряжённое к сопряжённому есть исходное).
(сопряжённое к сопряжённому есть исходное).



 , где
, где  — произвольный многочлен с вещественными коэффициентами.
— произвольный многочлен с вещественными коэффициентами.

 .
.


