Числа и множества. Числа и цифры. Римская буквенная нумерация. Позиционная система счисления (двоичная, десятичная).
A) 20700 B) 23307 C) 22222 D) 18000 E) 22111
Числа и множества. Числа и цифры. Римская буквенная нумерация. Позиционная система счисления (двоичная, десятичная). Число— основное понятие математики, используемое для количественной характеристики, сравнения и нумерации объектов. Цифры — система знаков («буквы») для записи чисел («слов») (числовые знаки). Слово «цифра» без уточнения обычно означает один из следующих десяти («алфавит») знаков: 0 1 2 3 4 5 6 7 8 9 (т. н. «арабские цифры»). Сочетания этих цифр порождают дву-(и более)значные коды и числа. Существуют также много других вариантов («алфавитов»): · римские цифры (I V X L C D M) · шестнадцатеричные цифры (0 1 2 3 4 5 6 7 8 9 A B C D E F) · цифры майя (от 0 до 19) · в некоторых языках, например, в древнегреческом, в иврите, в церковнославянском, существует система записи чисел буквами и др.
Позиционная система счисления (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Двоичная система счисления — позиционная система счисления с основанием 2. Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Положительные целые числа (без знака) записываются в виде:
где: · · · · · · · ·
Десятичная система счисления — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3,4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:
Обычно для ненулевого числа x требуют, чтобы старшая цифра Например, число сто три представляется в десятичной системе счисления в виде:
С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:
где n — число разрядов целой части числа, m — число разрядов дробной части числа.
Натуральные, простые, отрицательные числа. Основные арифметические действия и законы. Законы ассоциативности (сочетательности), коммутативности и дистрибутивности (распределительности). Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). Существуют два подхода к определению натуральных чисел — числа, используемые при: · перечислении (нумеровании) предметов (первый, второй, третий, …); · обозначении количества предметов (нет предметов, один предмет, два предмета, …). Принят в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств. Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются. Множество всех натуральных чисел принято обозначать знаком Множество 1. 2. Если 3. 4. Если 5. Аксиома индукции. Пусть если (Если некоторое высказывание Перечисленные аксиомы отражают наше интуитивное представление о «натуральном ряде». Простое число — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел. В теории колец простым числам соответствуют неприводимые элементы. Последовательность простых чисел начинается так: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137,139, 149, 151, 157, … (последовательность A000040 в OEIS, см. также список простых чисел) · Если · Кольцо вычетов · Характеристика каждого поля — это ноль или простое число. · Если · Если · Если · Натуральное · Если · Ряд чисел, обратных к простым, расходится. Более того, при
· Любая арифметическая прогрессия вида · Всякое простое число, большее 3, представимо в виде · Если · Теорема Грина-Тао. Существуют сколь угодно длинные конечные арифметические прогрессии, состоящие из простых чисел. · Никакое простое число не может иметь вид · Никакое простое число не может иметь вид · Существуют многочлены, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. Одним из примеров является многочлен
содержащий 26 переменных и имеющий степень 25. Наименьшая степень для известных многочленов такого типа — 5 при 42 переменных; наименьшее число переменных — 10 при степени около 1,6·1045. Этот результат является частным случаем доказанной Юрием Матиясевичем диофантовости любого перечислимого множества. Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля. Все отрицательные числа, и только они, меньше, чем ноль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим. Для каждого натурального числа n существует одно и только одно отрицательное число, обозначаемое -n, которое дополняет n до нуля:
Оба числа называются противоположными друг для друга. Вычитание целого числа a из другого целого числа b равносильно сложению b с противоположным для a:
При делении с остатком частное может иметь любой знак, но остаток, по соглашению, всегда неотрицателен (иначе он определяется не однозначно). Например, разделим −24 на 5 с остатком:
Ассоциативность (сочетательность, сочетательный закон) — свойство сложения и умножения чисел, выражаемое тождествами (а + b) + с = = а + (b + с) и (аb) с = a (bc).
Для ассоциативной операции результат вычисления Закон коммутативности - общее название логических законов, позволяющих менять местами высказывания, связанные конъюнкцией ("и"), дизъюнкцией ("или"), эквивалентностью ("если и только если") и др. Эти законы аналогичны алгебраическим законам коммутативности для умножения, сложения и др., по которым результат умножения не зависит от порядка множителей, сложения - от порядка слагаемых и т. д. Символически 3. к. для конъюнкции и дизъюнкции записываются так (р, q - некоторые высказывания, & - конъюнкция, v - дизъюнкция, = - эквивалентность): (p&q) = (q&p), р и q тогда и только тогда, когда q и р; (pvq) = (qvp), р или q, если и только если q или р.
Дистрибутивность, также распределительность — свойство согласованности двух бинарных операций, определённых на одном и том же множестве. Говорят, что две бинарные операции + и × удовлетворяют свойству дистрибутивности, если для любых трех элементов
Если операция × является коммутативной, то свойства дистрибутивности слева и справа совпадают. Аддитивная и мультипликативные операции в кольцах и полях по определению удовлетворяют свойству дистрибутивности. Если операции сложения и пересечения для односторонних идеалов некоторого кольца (или подмодулей некоторого модуля) удовлетворяют свойству дистрибутивности, то говорят о дистрибутивном кольце (или дистрибутивном модуле).
|


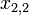 — представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),
— представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),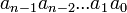 — запись числа, строка цифровых знаков,
— запись числа, строка цифровых знаков,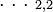 — обозначение основания системы кодирования и основания системы счисления,
— обозначение основания системы кодирования и основания системы счисления, — количество цифр (знаков) в числе x2,2,
— количество цифр (знаков) в числе x2,2, — порядковый номер цифры,
— порядковый номер цифры,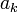 — цифры числа x2,2 из множества a={0,1}, в двоичной системе счисления основание системы кодирования равно 2,
— цифры числа x2,2 из множества a={0,1}, в двоичной системе счисления основание системы кодирования равно 2, — основание показательной весовой функции, основание системы счисления,
— основание показательной весовой функции, основание системы счисления, — весовая показательная функция, создающая весовые коэффициенты.
— весовая показательная функция, создающая весовые коэффициенты. , где
, где 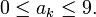
 в десятичном представлении x была также ненулевой.
в десятичном представлении x была также ненулевой.
 , то есть, всего
, то есть, всего  различных чисел.
различных чисел.
 . Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число.
. Множество натуральных чисел является бесконечным, так как для любого натурального числа найдётся большее его натуральное число. будем называть множеством натуральных чисел, если зафиксирован некоторый элемент
будем называть множеством натуральных чисел, если зафиксирован некоторый элемент  (единица) и функция
(единица) и функция  (функция следования) так, что выполнены следующие условия
(функция следования) так, что выполнены следующие условия является натуральным числом);
является натуральным числом); , то
, то 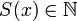 (Число, следующее за натуральным, также является натуральным);
(Число, следующее за натуральным, также является натуральным); (1 не следует ни за каким натуральным числом);
(1 не следует ни за каким натуральным числом); и
и  , тогда
, тогда  (если натуральное число
(если натуральное число  непосредственно следует как за числом
непосредственно следует как за числом  , так и за числом
, так и за числом  , то
, то 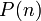 — некоторый одноместный предикат, зависящий от параметра — натурального числа
— некоторый одноместный предикат, зависящий от параметра — натурального числа  . Тогда:
. Тогда: и
и  , то
, то 
 верно для
верно для  (база индукции) и для любого
(база индукции) и для любого  (индукционное предположение), то
(индукционное предположение), то  — простое, и
— простое, и  , то
, то  является полем тогда и только тогда, когда
является полем тогда и только тогда, когда  делится на
делится на  — конечная группа с
— конечная группа с  элементов, то
элементов, то  , то
, то  для некоторого целого
для некоторого целого  (теоремы Силова).
(теоремы Силова). является простым тогда и только тогда, когда
является простым тогда и только тогда, когда  делится на
делится на  — натуральное, то существует простое
— натуральное, то существует простое  (постулат Бертрана).
(постулат Бертрана).

 , где
, где  — целые взаимно простые числа, содержит бесконечно много простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).
— целые взаимно простые числа, содержит бесконечно много простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).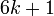 или
или  , где
, где  — простое, то
— простое, то  кратно 24 (справедливо также для всех нечётных чисел, не делящихся на 3).
кратно 24 (справедливо также для всех нечётных чисел, не делящихся на 3). , где n >2, k >1. Иначе говоря, число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, бо́льшим 2. Из этого следует также, что если простое число имеет вид
, где n >2, k >1. Иначе говоря, число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, бо́льшим 2. Из этого следует также, что если простое число имеет вид  , то k — простое (см. числа Мерсенна).
, то k — простое (см. числа Мерсенна). , где n >1, k >0. Иначе говоря, число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, бо́льшим 1.
, где n >1, k >0. Иначе говоря, число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, бо́льшим 1.


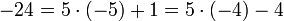 .
. , обладающая ассоциативностью (лат. associatio — соединение), или сочетательностью:
, обладающая ассоциативностью (лат. associatio — соединение), или сочетательностью: для любых элементов
для любых элементов  .
. не зависит от порядка вычисления (расстановки скобок), и потому позволяется опускать скобки в записи. Для неассоциативной операции выражение
не зависит от порядка вычисления (расстановки скобок), и потому позволяется опускать скобки в записи. Для неассоциативной операции выражение  в общем случае не определено.
в общем случае не определено.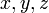 :
: — дистрибутивность слева;
— дистрибутивность слева; — дистрибутивность справа.
— дистрибутивность справа.


