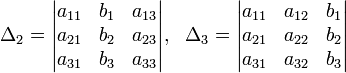Решение системы линейных уравнений с помощью определителей. Формулы Крамера.Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевымопределителем основной матрицы (причём для таких уравнений решение существует и единственно). Назван по имени Габриэля Крамера (1704–1752), придумавшего метод. Описание метода Для системы
с определителем матрицы системы
(i-ый столбец матрицы системы заменяется столбцом свободных членов).
В этой форме формула Крамера справедлива без предположения, что Пример Система линейных уравнений:
Определители:
Решение:
Пример:
Определители:
|
линейных уравнений с 
, отличным от нуля, решение записывается в виде
и 
, либо набор 
состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом. В этом виде формула Крамера используется, например, при доказательстве формулы для определителя Грама и Леммы Накаямы.
