Вектор в арифметическом n-мерном пространстве
Является частным случаем определения вектора в абстрактной алгебре. Если в качестве  взять поледействительных чисел с операциями сложения и умножения.
взять поледействительных чисел с операциями сложения и умножения. 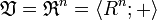 , где
, где  — декартова степеньмножества R; для
— декартова степеньмножества R; для  операцию «+» зададим следующим образом:
операцию «+» зададим следующим образом:  , нейтральный элемент:
, нейтральный элемент:  =(0,…,0), обратный элемент:
=(0,…,0), обратный элемент:  ; операцию умножения на скаляр:
; операцию умножения на скаляр:  . Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства
. Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства  над полем действительных чисел
над полем действительных чисел  .
.
n-мерное пространство задается как  — декартова степень множества действительных чисел, точка — как кортеж
— декартова степень множества действительных чисел, точка — как кортеж  длины n из действительных чисел, что соответствует определению пространства как множества точек.
длины n из действительных чисел, что соответствует определению пространства как множества точек.
Вектор в планарной евклидовой геометрии (связанный вектор) — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора.
Два вектора равны, если разности по каждой из координат с одинаковыми номерами конечной и начальной точки для этих векторов равны. Эти разности называются пространственными координатами вектора.
Свободный вектор задается классом всех равных связанных векторов и полагается равным каждому из этих связанных векторов и таким образом может быть определен как вектор в арифметическом пространстве (кортеж чисел длины n (пространственных координат равных ему связанных векторов) с операциями сложения и умножения на скаляр).
Результатом операций со связанными векторами принимается вектор, начальная точка которого совпадает с начальной точкой первого слагаемого при сложении векторов и начальной точке исходного вектора при умножении вектора на скаляр.
Нуль-вектор — вектор, начало и конец которого совпадают.
Также существует более распространенное определение вектора как направленного отрезка, но оно требует определения прямой и отрезка в n-мерном пространстве.
Прямая, на которой лежит ненулевой вектор  с началом в точке
с началом в точке  , заданный свободным вектором с пространственными координатами
, заданный свободным вектором с пространственными координатами  — множество точек
— множество точек  , удовлетворяющее условию:
, удовлетворяющее условию:
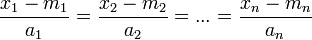
Отрезок MN — множество всех точек O(удовлетворяющих условию  ), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
При введение скалярного произведения, угла и длины вектора, задающей расстояние между двумя точками как расстояние между начальной и конечной точками вектора(как показано ниже([1], [2], [3])) векторное пространство  становится евклидовым нормированным пространством и при n=3 соответствует модели физического трехмерного пространства; при n=2 — плоскости этого пространства; при n=1 точка соответствует числу на числовой прямой, свободный вектор — разности двух чисел, а длина вектора соответствует модулю; при n=0 существует только одна точка(задается пустым кортежем), декартово произведение содержит только пустой кортеж, соответственно пространство представляет собой точку, есть только нулевой вектор; пространство при n>3 не имеет наглядной геометрической интерпретации, так как физическое пространство трёхмерно.
становится евклидовым нормированным пространством и при n=3 соответствует модели физического трехмерного пространства; при n=2 — плоскости этого пространства; при n=1 точка соответствует числу на числовой прямой, свободный вектор — разности двух чисел, а длина вектора соответствует модулю; при n=0 существует только одна точка(задается пустым кортежем), декартово произведение содержит только пустой кортеж, соответственно пространство представляет собой точку, есть только нулевой вектор; пространство при n>3 не имеет наглядной геометрической интерпретации, так как физическое пространство трёхмерно.
Скалярное произведение определяется по формуле: 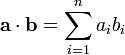 , [1]
, [1]
(где  — пространственные координаты векторов
— пространственные координаты векторов  )
)
Длина вектора:  , [2]
, [2]
(где  — пространственные координаты вектора.)
— пространственные координаты вектора.)
Угол между двумя векторами  (где
(где  — пространственные координаты векторов
— пространственные координаты векторов  ) определяется через скалярное произведение:
) определяется через скалярное произведение:
 , [3]
, [3]

 взять поледействительных чисел с операциями сложения и умножения.
взять поледействительных чисел с операциями сложения и умножения. 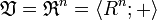 , где
, где  — декартова степеньмножества R; для
— декартова степеньмножества R; для  операцию «+» зададим следующим образом:
операцию «+» зададим следующим образом:  , нейтральный элемент:
, нейтральный элемент:  =(0,…,0), обратный элемент:
=(0,…,0), обратный элемент:  ; операцию умножения на скаляр:
; операцию умножения на скаляр:  . Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства
. Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства  над полем действительных чисел
над полем действительных чисел  .
. длины n из действительных чисел, что соответствует определению пространства как множества точек.
длины n из действительных чисел, что соответствует определению пространства как множества точек. с началом в точке
с началом в точке  , заданный свободным вектором с пространственными координатами
, заданный свободным вектором с пространственными координатами  , удовлетворяющее условию:
, удовлетворяющее условию: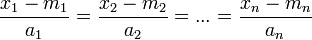
 ), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.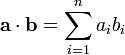 , [1]
, [1] — пространственные координаты векторов
— пространственные координаты векторов  )
) , [2]
, [2] — пространственные координаты вектора.)
— пространственные координаты вектора.) , [3]
, [3]


