Прямоугольные координаты вектора
Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца[6]. · Таким образом, например, координаты (x,y) на рис.1 являются координатами вектора Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов: 1. Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесенного так, что его начало совпадает с началом координат, - это координаты его конца. 2. Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала. · Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси. В прямоугольных координатах очень просто записываются все операции над векторами: · Сложение и умножение на скаляр:
или
или
а отсюда и вычитание и деление:
или
или
(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат). · Скалярное умножение:
или
(Только в прямоугольных координатах с единичным масштабом по всем осям). · Через скалярное произведение - длину вычисление длины вектора
и угла между векторами
· Внешнее умножение:
для любой размерности пространства, · Векторное умножение (только для трехмерного же пространства, на котором оно и определено):
Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.
Трилинейные координаты тесно связаны с барицентрическими координатами. А именно, если
её трилинейные координаты. Трилинейные координаты, как и барицентрические, определены с точностью до пропорциональности. Для точки В трилинейных координатах изогональное сопряжение задаётся формулой
Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой Точка · · · При использовании в физических науках и технике международный стандартISO 31-11 рекомендует использовать обозначения Некоторые математики используют Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось
|

 .
.



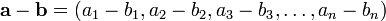










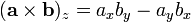
 — барицентрические координаты точки
— барицентрические координаты точки  относительно треугольника
относительно треугольника  , то
, то
 . Это означает, что в качестве трилинейных координат можно взять расстояния от точки
. Это означает, что в качестве трилинейных координат можно взять расстояния от точки  лежат по одну сторону от прямой
лежат по одну сторону от прямой  , то
, то  , а если по разные, то
, а если по разные, то  .
. . В связи с этим трилинейные координаты часто бывают удобны при работе с изогональным сопряжением.
. В связи с этим трилинейные координаты часто бывают удобны при работе с изогональным сопряжением.
 ), которая задаёт высоту точки над плоскостью.
), которая задаёт высоту точки над плоскостью. даётся как
даётся как  . В терминах прямоугольной системы координат:
. В терминах прямоугольной системы координат: — расстояние от
— расстояние от  до
до  , ортогональной проекции точки
, ортогональной проекции точки  . Или то же самое, что расстояние от
. Или то же самое, что расстояние от  .
. — угол между осью
— угол между осью  .
.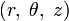 .
. , а в цилиндрических — очень простое уравнение
, а в цилиндрических — очень простое уравнение  . Отсюда и идёт для данной системы координат имя «цилиндрическая».
. Отсюда и идёт для данной системы координат имя «цилиндрическая».



