Сложение
Операцию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый их которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и геометрически фундаментальное, удобно для сложения любого количества векторов, однако правило параллелограмма более удобно для фиксированных или скользящих векторов, так как не требует переноса второго слагаемого (что в принципе могло бы смущать или запутывать в этих случаях) для построения суммы, то есть удобно для сложения векторов с началом в одной точке, в добавок имея то преимущество, что в нем более очевидно равноправие слагаемых; координатное же определение, являясь простым и удобным, бывает очень полезно для вычислений.
Правило треугольника. Для сложения двух векторов Правило параллелограмма. Для сложения двух векторов Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:
(Могут быть использованы прямоугольные или косоугольные координаты; правило сложения остаются одинаковыми для обоих этих типов координат). · Модуль (длину) вектора суммы Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма. Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма. Сложение коллинеарных скользящих векторов Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные векторы. Пусть, например, надо сложить скользящие векторы
Прямые, на которых расположены векторы Таким образом, под суммой векторов
|

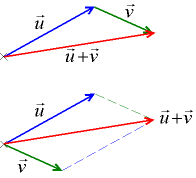 Два вектора u, v и вектор их суммы
Два вектора u, v и вектор их суммы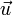 и
и  по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).
по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).

 можно вычислить, например, используя теорему косинусов
можно вычислить, например, используя теорему косинусов 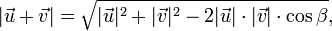 где
где  — угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого. Или:
— угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого. Или:  где
где  — угол между векторами (выходящими из одной точки).
— угол между векторами (выходящими из одной точки).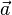 и
и  , расположенные на параллельных прямых. Добавим к ним векторы
, расположенные на параллельных прямых. Добавим к ним векторы  и
и  , расположенные на одной прямой. Прямые, на которых расположены векторы
, расположенные на одной прямой. Прямые, на которых расположены векторы 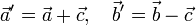
 и
и  , пересекаются всегда, за исключением случая, когда векторы
, пересекаются всегда, за исключением случая, когда векторы  образуют пару (векторов).
образуют пару (векторов).


