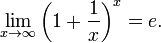Вычислительная сложность
Метод Крамера требует вычисления 30. Предел функции. Теоремы о пределах (предел суммы и разности, произведения частного функций). Приделы некоторых функций (, Предел функции (предельное значение функции) в заданной точке,предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится. Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят). В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств. Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности». Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности. Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной (в данной точке). Предел функции — одно из основных понятий математического анализа. Основные теоремы о пределах функций
Поэтому нельзя указать никакого числа b, к которому стремились бы значения этой функции. Другой пример. Пусть
График этой функции представлен на рисунке 304.
Когда значений аргумента х приближаются к 0, оставаясь отрицательными, соответствующие значения функции стремятся к 1. Когда значения аргумента х приближаются к 0, оставаясь положительными, соответствующие значения функции стремятся к —2. В самой же точке х = 0 функция обращается в 0. Очевидно, что указать одно какое-нибудь число, к которому стремились бы все значения у при приближении х к 0, нельзя. Поэтому данная функция не имеет предела при х —> 0. Говоря в дальнейшем о пределе функции, мы всегда будем предполагать, что этот предел существует. Предположение о существовании предела
Очевидно, что предел
Если функция у = f (х) удовлетвoряет условию
то она называется непрерывной в точке х = а. Если же указанное условие не выполняется, то функция f (х) называется разрывной в точке х = а. ' Все элементарные функции (например, у = хп, у = sin х, у = tg х, у = tg2 х + tg х и т. д.) непрерывны в каждой точке, в которой они определены. Функция у = f (х) называется непрерывной в интервале [ а, b ], если она непрерывна в каждой точке этого интервала. Например, функция у = tg x непрерывна в интервале[— π/ 4 , π/ 4 ], функции у = sin x и y = cos x непрерывны в любом интервале и т. д. Приведем без доказательства основные теоремы о пределах функций. Эти теоремы вполне аналогичны тем, которые мы рассматривали (также без доказательства) ранее при изучении пределов числовых последовательностей. 1. Предел константы равен самой этой константе:
2. Постоянный множитель можно выносить за знак предела:
3. Предел суммы (разности) функций равен сумме (разности) пределов этих функций:
4. Предел произведения функций равен произведению пределов этих функций:
5. Предел отношения двух функций равен отношению пределов этих функций, если только предел делителя не равен нулю:
Пример 1. Найти
При х —> 3 числитель и знаменатель данной дроби стремятся к нулю. Поэтому непосредственное применение теоремы о пределе частного здесь невозможно. Однако данную дробь можно сократить:
(Обратите внимание на следующую важную особенность, характерную для рассмотренного примера. Когда мы говорим о пределе · Первый замечательный предел:
· Второй замечательный предел:
|

 определителей размерности
определителей размерности  . При использовании метода Гаусса для вычисления определителей, метод имеет временную сложность порядка
. При использовании метода Гаусса для вычисления определителей, метод имеет временную сложность порядка  , что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью
, что хуже, чем если бы метод Гаусса напрямую использовался для решения системы уравнений. Поэтому метод считался непрактичным. Однако в 2010 году было показано, что метод Крамера может быть реализован со сложностью  , сравнимой со сложностью метода Гаусса.
, сравнимой со сложностью метода Гаусса. ,
,  …). Первый и второй замечательные пределы.
…). Первый и второй замечательные пределы. f (х). Так, например, при x —> π/ 2 значения функции у = tg х (рис. 303) или неограниченно растут (при х < π/ 2), или неограниченно убывают (при х > π/ 2).
f (х). Так, например, при x —> π/ 2 значения функции у = tg х (рис. 303) или неограниченно растут (при х < π/ 2), или неограниченно убывают (при х > π/ 2).



 f (х) существует и равен 1. Но в самой точке х = 0 функция принимает значение, равное 2. Поэтому в данном случае
f (х) существует и равен 1. Но в самой точке х = 0 функция принимает значение, равное 2. Поэтому в данном случае
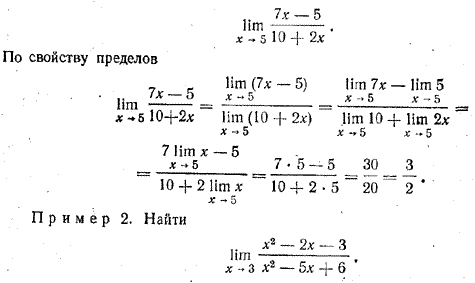

 определена лишь для положительных значений х. Поэтому, рассматривая предел этой функции, мы фактически предполагаем, что х —> 0, оставаясь все время положительным. В подобных случаях говорят не просто о пределе, а об одностороннем пределе.
определена лишь для положительных значений х. Поэтому, рассматривая предел этой функции, мы фактически предполагаем, что х —> 0, оставаясь все время положительным. В подобных случаях говорят не просто о пределе, а об одностороннем пределе.