Тангенс угла наклона касательной прямой
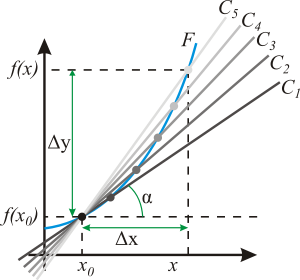
Геометрический смысл производной. На графике функции выбирается абсцисса x0 и вычисляется соответствующая ордината f(x0). В окрестности точки x0 выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C5). Расстояние Δx = x — x0 устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C5 — C1). Тангенс угла α наклона этой касательной — и есть производная в точке x0. Если функция
Функция Физический смысл производной. Вычисление скорости движения точки. Скорость изменения функции Пусть Вообще производная функции
Правила дифференцирования. Теорема о производных от суммы (разности), произведения и частного двух дифференцируемых функций.
|
имеет конечную производную в точке 
то в окрестности 
её можно приблизить линейной функцией
называется касательной к 
в точке 
Число 
является угловым коэффициентом или тангенсом угла наклонакасательной прямой.
— закон прямолинейного движения. Тогда 
выражает мгновенную скорость движения в момент времени 
Вторая производная 
выражает мгновенное ускорение в момент времени 
в точке 
выражает скорость изменения функции в точке 
