Понятие распределения вероятностей случайных событий. Схема независимых испытаний. Формула Бернулли. Повторные независимые испытания. Формула Бернулли с выводом.Если вер-ть наступления события А в каждом испытании не меняется в завис-ти от исходов других, то такие испытания наз-ся независ-ми относит-но события А. Если независ-е повторные испытания проводятся при одном и том же комплексе условий, то вер-ть наступления соб-я А в каждом испытании одна и та же. Последовательность испытаний, в кот 1 и те же события происходят с одинаковой вер-ю, наз последовательностью независ-х испытаний. А соб, кот может иметь место с вер-ю Р(А) в любом из n испытаний. А ->P(A) P(A)=P – вер-ть осущ-я события в каждом отдельном событии
Поставим задачу опр-я вер-ти m-кратного осуществл-я события А в серии из n испытаний. Pm,n – вер-ть m-кратного осуществл-я события в серии n испытаний. Условно рез-ты послед-ти независ-х испытаний м\б представлены: Теорема: Если вер-ть А в каждом испытании постоянна, то вер-ть Pm,n того, что событие А наступит m раз в n независимых испытаниях, равна
|
- вер-ть неоосущ-я событий; 
; 
; 
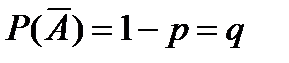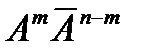, тк в послед-ти независ-х испытаний, каждое из соб независимо и для m-кратного осуществл события они должны произойти совместно, соотв-я вер-ть опр-ся по ф-ле вер-ти произведения 
. Предполагая, что возможен и др порядок следования А и 
на множестве n испытаний, а кол-во комбинаций = 
, получим ф-лу m-кратного осуществ-я соб А в серии из n испытаний: 
à Формула Бернулли. Используется при условии, что событие происходит многократно.
, где q=1-p ф Бернулли применяется в тех случаях, когда число опытов невелико, а вероятности появления достаточно велики. 
