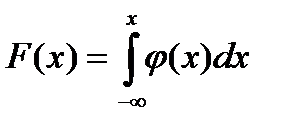Функция распределения непрерывной случайной величины и ее свойства. Функции плотности распределения. Мода, медиана. Начальные и центральные моменты. Примеры.
Функция распределения НСВ:
ФРНСВ наз вер-ть т\ч она примет значение меньшее заданного.
Основные свойства ф-ии распределения НСВ: С1. С3. С4. Вер-ть т\ч НСВ примет значение из интервала, равна приращению ф-ии на этом интервале 1) 2) Скорость изменения функции распределения хар-ся плотностью распр-я. Обозначается символом Свойства плотности распр-я (ПР): С1. ПР – неотрицательная функция. С2. Вер-ть попадания НСВ в интервал [a,b] равна определённому интегралу от её плотности вер-ти в пределах от a до b, т.е. С3. Ф-я распр НСВ м\б выражена через плотность вер-ти по формуле: С4. Несобственный интеграл в бесконечных пределах от плотности вер-ти НСВ =1. Мода Мо(Х) случ. величины X - наз-ся ее наиболее вероятное значение (для которого вер-сть рi или плотность вер-сти φ(х) достигает max). Медиана Ме(Х) непрерывной случ. величины X наз-тся такое ее значение, для которого Р(X<Me(X))=P(X>Me(X))=0,5, т.е. вер-сть того, что X примет значение, < Ме(Х) или > ее, одна и та же и = 0,5. Геометрически: вертикальная прямая, проходящая через точку х=Ме(Х), делит площадь фигуры под кривой распределения на 2 равные части. Начальным моментом k-го порядка случ. велич X наз-ся мат. ожидание k-й степени этой величины: νk=M(X^k). Для непрерывн случ велич: νk=∫х^k φ(x)dx (интеграл от -∞ до +∞). Центральный моментом k-го порядка случ. велич. X наз-тся матю ожидание k-й степени отклонения X от ее мат. ожидания: μk=M[X-M(X)]^k. Для непрерывной случ велич: μk= ∫(х-М(Х))^k φ(x)dx (интеграл от -∞ до +∞).
|

 , в качестве способа задания НСВ используется функция распределения НСВ.
, в качестве способа задания НСВ используется функция распределения НСВ. -обознач ф-ии распр в-тей
-обознач ф-ии распр в-тей à
à 
 С2.
С2. 



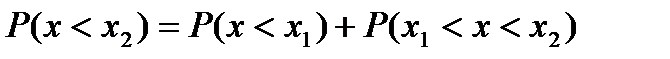
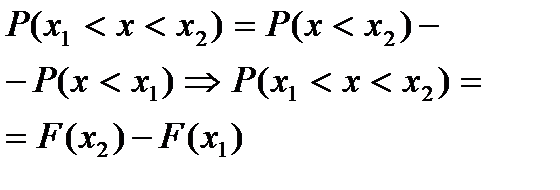
 . Плотностью вер-ти (плотностью распр-я)
. Плотностью вер-ти (плотностью распр-я)  НСВ Х наз-ся производная её ф-ии распр-я
НСВ Х наз-ся производная её ф-ии распр-я 
 ;
;