Модель БКШ.
Суммарный спин куперовской пары равен нулю. Однако куперовскую пару нельзя считать обыкновенной бозе-частицой, поскольку радиус связанного состояния двух электрон в пределе слабого взаимодействия существенно больше среднего расстояния между электронами в металле, т. е. куперовские пары сильно перекрываются друг с другом и влияют друг на друга. Поэтому более точно говорить о парных корреляциях в вырожденном Ферми-газе. При этом спаривание происходит не в обычном координатном пространстве, а в импульсном k -пространстве. Теория БКШ описывает сверхпроводящее состояние вырожденного Ферми-газа, обусловленное такими парными корреляциями. Выше мы установили, что электроны в состояниях
Обозначим через
Аналогичную вероятность при рассеянии
Обозначим через
Запишем выражение для средней энергии сверхпроводящего состояния
Будем считать, что матричный элемент взаимодействия электронов отличен от нуля только в узком слое толщиной
Для средней энергии имеем:
С учетом тождества
получим следующее уравнение
Введем параметр, который далее будем называть параметром порядка:
В результате полученное уравнение принимает вид:
С помощью преобразований:
приведем его к виду:
где мы ввели еще один важный параметр
Выбирая физически содержательный (
При этом если График зависимости функции заполнения частиц от квазиимпульса приведен на рисунке:
Исходное уравнение определяет параметр порядка Рассмотрим решение уравнения самосогласования для параметра порядка:
Введем эффективную константу взаимодействия:
и проинтегрируем уравнение самосогласования
В результате для параметра порядка находим:
Полученное выражение напоминает выражение для энергии связи куперовской пары, но отличается отсутствием двойки в показателе экспоненты. Таким образом параметр порядка существенно превышает по величине энергию связи одиночной куперовской пары, что обусловлено коллективной природой куперовского спаривания в вырожденном Ферми-газе.
|

 могут образовывать связанные состояния. Обозначим через
могут образовывать связанные состояния. Обозначим через  вероятность того, что пара состояний
вероятность того, что пара состояний  занята. Соответственно через
занята. Соответственно через  - вероятность того, что пара
- вероятность того, что пара  .
.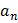 амплитуду вероятности того, что состояния
амплитуду вероятности того, что состояния  – пусты:
– пусты: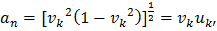 .
.
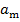
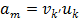 .
. с учетом рассеяния
с учетом рассеяния
 вблизи поверхности Ферми, и заменим его в этой области константой:
вблизи поверхности Ферми, и заменим его в этой области константой:
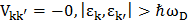
 .
.
 .
. .
. .
. ,
,
 ,
, .
. ) корень уравнения получим решение:
) корень уравнения получим решение: .
. то в силу
то в силу 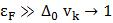 .
.
 через
через  и
и 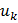 , которые, в свою очередь, зависят от
, которые, в свою очередь, зависят от 






