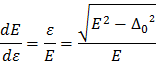Спектр элементарных возбужденийОпределим энергию, необходимую для создания элементарного возбуждения в сверхпроводящем состоянии. Рассмотрим пару электронов в состоянии (
Для wq можно записать
Где фигурирует введенный выше параметр Eq. Рассмотрим ситуацию, когда в сверхпроводник добавлен 1 неспаренный электрон в состоянии q. Энергия неспаренного электрона и есть энергия элементарного возбуждения:
Таким образом мы получили, что введенный выше параметр Eq есть ничто иное, как энергия элементарных возбуждений в сверхпроводнике. При этом минимальная энергия возбуждений соответствует минимальному значению :
Здесь линейная функция отвечает линеаризованному закону дисперсии электронов (без учета взаимодействия)
Если неспаренная частица не привносится в сверхпроводник извне, то для создания элементарных возбуждений необходимо разорвать куперовскую пару. Минимальная энергия, необходимая для разрыва куперовской пары равна 2
В отличие от полупроводника, где энергетическая щель, как правило, отвечает дискретному набору точек (или одной точке) в зоне Бриллюэна, в сверхпроводнике энергетическая щель возникает на всей поверхности Ферми. В полупроводнике плотность состояний на краю разрешенной зоны (или, что то же самое, на краю щели) обращается в нуль. В сверхпроводнике из-за того, что краю щели отвечает целая поверхность, плотность состояний g(E) имеет особенность (при
Здесь мы учли соотношение:
График зависимости плотности состояний от энергии элементарных возбуждений приведен на рисунке вместе с графиком зависимости энергии элементарных возбуждений от волнового вектора. Наличие особенности плотности состояний на краю щели послужило ключом к объяснению многих необычных физических свойств сверхпроводников.
Для энергии основного состояния сверхпроводника W0 можно получить следующее выражение:
|
). Обозначим через 
энергию пары.
,
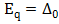. Для Eq вблизи уровня Ферми электронов (которые уже не есть элементарные возбуждения) имеем следующий график
. Процессу создания элементарных возбуждений можно сопоставить следующую энергетическую диаграмму, которая формально подобна закону дисперсии полупроводника:
):
.
