Задача Купера. Куперовские пары.
Покажем, что парное взаимодействие электронов, которое имеет характер притяжения, приводит к образованию их связанного состояния. Это не так очевидно, поскольку речь идет о трехмерной системе. Как известно из квантовой механики, связанное состояние частицы на притягивательном потенциале имеет место при любом, даже сколь угодно слабом потенциале, только в одномерных и двумерных системах. В трехмерной ситуации связанное состояние образуется только в случае достаточно сильного потенциала. Рассмотрим уравнение Шредингера для двух взаимодействующих электронов, находящихся над поверхностью Ферми:
здесь в операторе εF кинетической энергии мы отсчитываем энергию от уровня Ферми:
Волновая функция пары невзаимодействующих электронов с противоположными импульсами имеет вид произведения двух плоских волн:
где
Электронам, находящимся в возбужденном состоянии над поверхностью Ферми, соответствует условие
Перегруппируем члены в уравнении Шредингера
Найдем среднее значение энергии:
Подставив в это соотношение выражение для волновой функции в виде суперпозиции по состояниям плоских волн, получим:
где матричный элемент энергии взаимодействия описывает рассеяние из состояния
Полученное интегральное уравнение в общем случае требует численного решения. Однако, если сделать некоторые допущения о виде ядра (матричного элемента взаимодействия), то можно получить аналитическое решение. Рассмотрим сепарабельное взаимодействие (допускающее разделение на множители) вида
Умножим обе части на
Здесь дискретная сумма k по выполняется по дискретным значениям квазиимпульса, определяемым граничными условиями Борна-Кармана (m1,2,3 –целые):
Соответственно, εk также принимает дискретный ряд значений. Решение этого уравнения удобно проанализировать графически. График правой части имеет вид, представленный на рисунке. Особенности графика соответствуют нулям знаменателя. Как следует из графика при λ>0 все решения расположены в области E>0 и описывают незначительный сдвиг уровней энергии из-за рассеяния. Вместе с тем при λ<0, т.е. при наличии межэлектронного притяжения, появляется дополнительное решение при E<0,

отвечающее связанному состоянию двух электронов. Это решение существует при любом сколь угодно слабом межэлектронном притяжении. Два электрона в связанном состоянии образуют куперовскую пару. Более точно определить энергию связанного состояния можно, решив уравнение на собственные значения. Выше мы установили, что межэлектронное притяжение действует в узком энергетическом слое вблизи поверхности Ферми. Пренебрегая угловой зависимостью матричного элемента взаимодействия, выберем определяющие его сомножители в следующем виде:
Перейдем в уравнении на собственные значения стандартным образом от суммирования к интегрированию в пределе бесконечного объема системы
где мы учли, что вблизи поверхности Ферми
и
Введем эффективную константу взаимодействия где
В результате находим для энергии связанного состояния
При стремлении эффективной константы взаимодействия к нулю энергия связанного состоянии экспоненциально по обратному параметру взаимодействия стремится к нулю. Именно таким поведением характеризуется энергия связанного состояния от глубины потенциальной ямы в двумерной системе. Данная аналогия имеет глубокий физический смысл и объясняет природу связанного состояния электронов. Электроны, движущиеся в узком слое вблизи поверхности Ферми можно считать эффективно двумерными. Поэтому в соответствии с общим результатом квантовой механики пара таких электронов образует связанное состояние при сколь угодно слабом взаимодействии.
|


 ,
, ,
,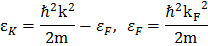
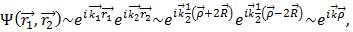

 . Ищем решение для волновой функции взаимодействующих электронов в виде произвольной суперпозиции таких состояний:
. Ищем решение для волновой функции взаимодействующих электронов в виде произвольной суперпозиции таких состояний: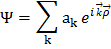

 .
. ,
, в состояние
в состояние  :
:
 ,
, .
. и просуммируем по k. Сокращая обе части на
и просуммируем по k. Сокращая обе части на  (при условии
(при условии 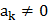 ), получим следующее уравнение для определения разрешенных значений энергии:
), получим следующее уравнение для определения разрешенных значений энергии: .
. .
.
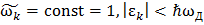



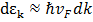 . Пусть межэлектронное взаимодействие отвечает притяжению:
. Пусть межэлектронное взаимодействие отвечает притяжению: .
.
 - эффективная плотность состояний на поверхности Ферми. Выполнив интегрирование, получим:
- эффективная плотность состояний на поверхности Ферми. Выполнив интегрирование, получим: ,
,



