Механическая аналогия.
Рассмотрим эквивалентную схему джозефсоновского перехода с учетом его емкости C. В последующих выкладках будем считать скорость света с=1.
В уравнение для тока следует добавить связанный с емкостью ток смещения:
В результате уравнение для фазы принимает фид
В таком виде уравнение для фазы полностью аналогично уравнению механического массивного маятника:
При этом имеет место следующее соответствие электрических и механических характеристик:
Момент силы тяжести
Если

Диссипативный ток при гистерезисе сохраняется вплоть до самых малых напряжений. Значение тока на обратной ветке ВАХ при нулевом напряжении называется током возврата. Глубину гистерезиса и величину тока возврата принято характеризовать с помощью так называемого параметра МакКамбера:
где:
Зависимость тока возврата от параметра МакКамбера имеет следующий вид:

Величины этого параметра определяет форму кривых гистерезиса ВАХ:
Макроскопические квантовые эффекты в Джозефсоновских переходах. Динамика Джозефсоновского перехода описывается уравнением математически идентичным уравнению движения физического маятника в классической механике. При этом джозефсоновская фаза (разность фаза параметров порядка на берегах джозефсоновского перехода, т.е. величина квантовая) играет роль аналогичную углу вращения маятника – сугубо классической переменной. Известно, что переход от классического описания физического маятника к квантово-механическому формально достигается путем применения процедуры квантования. Возникает вопрос: имеют ли физический смысл дискретные уровни энергии и квантованные состояния, возникающие при формальном применении подобной процедуры к джозефсоновскому переходу? Ответ на этот вопрос оказался положительным, и эффекты, связанные с квантованием состояний джозефсоновского перехода экспериментально наблюдались. Поскольку джозефсоновский переход в отличие от элементарных частиц, атомов и молекул, поведение которых подчиняется законам квантовой механики, представляет собой макроскопический объект, такие эффекты получили название макроскопических квантовых эффектов. Их также иногда называют вторичными квантовыми эффектами, поскольку сам по себе эффект Джозефсона представляет собой квантовое явление. При квантовании физического маятника роль, аналогичную соотношению неопределенности Гейзенберга для координаты и импульса
играет соотношение для фазы и момента вращения M
В состоянии с ограниченным по абсолютной величине моментом вращения фаза точно не определена, что приводит, в частности, к ненулевому значению минимальной энергии квантового маятника (нулевые колебания). Аналогично тому, как для частицы с массой m квантовые свойства усиливаются с уменьшением массы, роль квантовых свойств физического маятника возрастает с уменьшением момента инерции J. С учетом установленного выше соответствия между характеристиками джозефсоновского перехода и физического маятника, приходим к выводу, что квантовые свойства джозефсоновского перехода усиливаются с уменьшением его емкости С.
С учетом квантования энергия джозефсоновского перехода уже не представляет собой непрерывную функцию фазы, а квантуется и принимает дискретные значения (см. рис.). Переход между квантованными состояниями, расположенными в различных локальных минимумах потенциальной энергии перехода может происходить как за счет термоактивации, так и за счет туннелирования. При туннелировании вырожденные по энергии уровни перехода должны расщепляться. Такое расщепление наблюдалось
экспериментально, что и послужило доказательством квантовой (вторичной квантовой) природы макроскопических состояний джозефсоновского перехода. Семинар 10. Микроскопическая теория сверхпроводимости БКШ. Сверхпроводимость как сверхтекучесть электронного газа. Изотопический эффект и электрон-фононное взаимодействие. Задача Купера и природа электрон-электронного притяжения. Модель БКШ и уравнение самосогласования для параметра порядка. Спектр элементарных возбуждений и плотность состояний. Кратко сформулируем основные положения и идеи микроскопической теории сверхпроводимости Бардина-Купера-Шриффера (БКШ). В основе теории БКШ лежит представление о формировании куперовских пар - связанных состояний двух электронов с противоположными спинами. Куперовские пары образуют сверхпроводящий конденсат, аналогично сверхтекучему конденсату бозонов, и сверхпроводимость можно трактовать как сверхтекучесть заряженных частиц. Природа сверхтекучести тесно связана с явлением бозе-конденсации. Бозе-конденсация возникает при достаточно низких температурах в газе частиц, подчиняющихся статистике Бозе-Эйнштейна, даже в отсутствие взаимодействия между ними. Бозе конденсат становится сверхтекучим при наличии слабого отталкивания между частицами. В сверхпроводнике куперовская пара двух электронов представляет собой бозон, однако этот бозон образован электронами проводимости, делокализованными частицами. Идея описать сверхпроводимость на языке бозонов и бозе-конденсата посещала многих ученых, но последовательная теория была построена только в 1957 г. (БКШ). Неожиданным в их теории оказалось то, что сами по себе куперовские пары образуются одновременно с образованием бозе-конденсата в точке сверхпроводникового перехода. Для образования куперовской пары два электрона должны
притягиваться друг к другу. Природа межэлектронного притяжения связана с электрон-фононным взаимодействием (испускание и поглощение электронами фононов – обмен фононами). Физически это можно представить себе следующим образом: отрицательно заряженный электрон на пути своего движения притягивает положительно заряженные ионы и вызывает их смещение из положения равновесия. Поскольку масса электрона много меньше массы иона (m<<M), электрон движется гораздо быстрее иона, и смещение иона сохраняется в течение некоторого времени после того, как электрон покидает окрестность иона. В результате вдоль траектории движения электрона образуется область положительного потенциала (потенциальная яма). Другой электрон, попадая в эту потенциальную яму, понижает свою энергию, что можно трактовать, как опосредованное через колебания решетки (фононы) эффективное межэлектронное притяжение. Поскольку потенциальная яма сохраняется некоторое время в отсутствие создавшего ее (первого) электрона, прямое кулоновское отталкивание электронов при таком процессе несущественно. Из сказанного ясно, что максимальный выигрыш в потенциальной энергии второго электрона будет иметь место, если его траектория повторяет траекторию первого электрона в противоположном направлении, т.е., импульсы двух электронов противоположны. В приведенной выше картине речь, фактически, идет о связанных колебаниях электронной и ионной плотностей. Оценим более конкретно характерный масштаб энергии электронов, при котором возможно эффективное взаимодействие их с ионами. Волновую функцию пары электронов можно записать в следующем виде:
Откуда для электронной плотности получаем
Таким образом для характерной частоты колебаний электронной плотности имеем
где
откуда следует, что при
Без учета взаимодействия полная энергия электронного газа равна его кинетической энергии. Основное состояние электронного газа при этом представляет собой сферу Ферми с резкой границей при энергии равной при энергии Ферми.
Рассмотрим роль взаимодействия и покажем, что с учетом взаимодействия резкая граница заполненных и незаполненных состояний уже не отвечает основному состоянию системы. Запишем волновую функцию системы
Соответственно, средняя энергия представляет собой сумму кинетической энергии и энергии взаимодействия
Если энергия взаимодействия отрицательна (
Для того, чтобы электроны имели возможность рассеиваться, часть состояний над поверхностью Ферми должна быть заполнена, а часть под поверхностью Ферми – пустыми. тем больше, чем больше количество возможных каналов рассеяния, т.е. чем больше объем той части фазового пространства, которая может участвовать в процессах рассеяния. Обозначим через
Для сферической поверхности Ферми максимальный объем фазового пространства достигается при
Таким образом, действительно, в соответствие с нашими качественными рассуждениями энергетически наиболее выгодно парное взаимодействие электронов с равными по величине и противоположно направленными импульсами.
|





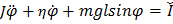




 (приложенный вращательный момент больше момента силы тяжести), единственный возможнй тип движения – поступательное вращение маятника. При уменьшении параметра Iдо значения меньше Icпоступательное вращения маятника может сохраниться в силу инерции. Для джозефсоновского перехода такая ситуация отвечает наличию гистерезиса на ВАХ, когда при токе, меньшем критического, на переходе имеется отличное от нуля напряжение и через него течет диссипативный ток.
(приложенный вращательный момент больше момента силы тяжести), единственный возможнй тип движения – поступательное вращение маятника. При уменьшении параметра Iдо значения меньше Icпоступательное вращения маятника может сохраниться в силу инерции. Для джозефсоновского перехода такая ситуация отвечает наличию гистерезиса на ВАХ, когда при токе, меньшем критического, на переходе имеется отличное от нуля напряжение и через него течет диссипативный ток.








 .
.



 . Обозначим через X смещение ионов из положения равновесия. Уравнение движения для X имеет вид:
. Обозначим через X смещение ионов из положения равновесия. Уравнение движения для X имеет вид: ,
, - собственная частота колебаний ионов (порядка дебаевской частоты), параметр f в правой части описывает силу кулоновского взаимодействия электронов и ионов. В результате для амплитуды смещений ионов находим:
- собственная частота колебаний ионов (порядка дебаевской частоты), параметр f в правой части описывает силу кулоновского взаимодействия электронов и ионов. В результате для амплитуды смещений ионов находим: ,
, электронные и ионный плотности колеблются синфазно, а при
электронные и ионный плотности колеблются синфазно, а при  - в противофазе. Взаимодействие двух электронов через обмен фононами, по сути, представляет собой процесс рассеяния. В силу принципа Паули в процессах рассеяния могут участвовать только электроны вблизи поверхности Ферми. Характерная частота колебаний электронной плотности при этом имеет порядок энергии электронных возбуждений вблизи поверхности Ферми. Таким образом синфазные колебания ионной и электронной плотностей возможны, если характерная энергия электронных возбуждений не превышает дебаевской энергии. Такие состояния располагаются в узком пояске вблизи поверхности Ферми шириной
- в противофазе. Взаимодействие двух электронов через обмен фононами, по сути, представляет собой процесс рассеяния. В силу принципа Паули в процессах рассеяния могут участвовать только электроны вблизи поверхности Ферми. Характерная частота колебаний электронной плотности при этом имеет порядок энергии электронных возбуждений вблизи поверхности Ферми. Таким образом синфазные колебания ионной и электронной плотностей возможны, если характерная энергия электронных возбуждений не превышает дебаевской энергии. Такие состояния располагаются в узком пояске вблизи поверхности Ферми шириной


 в виде разложения по базису одночастичных состояний:
в виде разложения по базису одночастичных состояний:
 – волновая функция одного электрона. Рассмотрим гамильтониан системы в виде суммы оператора кинетической энергии и члена, описывающего взаимодействие:
– волновая функция одного электрона. Рассмотрим гамильтониан системы в виде суммы оператора кинетической энергии и члена, описывающего взаимодействие:
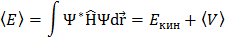
 ), т.е. отвечает притяжению частиц, то энергия с учетом взаимодействия может оказаться ниже, чем в отсутствие взаимодействия. Член с взаимодействием связывает различные квантовые состояния, т.е. описывает процесс рассеяния:
), т.е. отвечает притяжению частиц, то энергия с учетом взаимодействия может оказаться ниже, чем в отсутствие взаимодействия. Член с взаимодействием связывает различные квантовые состояния, т.е. описывает процесс рассеяния: .
. импульсы электронов до рассеяния. В результате рассеяния они приобретают импульсы::
импульсы электронов до рассеяния. В результате рассеяния они приобретают импульсы::  :
:





