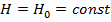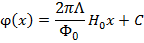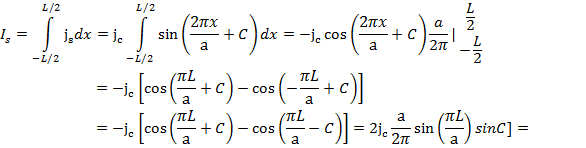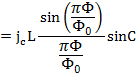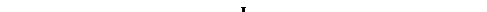Влияние магнитного поля на Джозефсоновский переход
Для возникновения эффекта Джозефсона необходимо наличие слабой связи двух сверхпроводников. Интересен вопрос, как на такую слабую связь влияет магнитное поле. Рассмотрим джозефсоновский контакт, плоскость с туннельной прослойкой толщиной t и шириной L. Пусть магнитное поле направлено вдоль оси z, а контакт находится в плоскости xz. Будем действовать стандартным образом: проведем разрывный контур C` в плоскости xy, на котором ток равен нулю (для этого контур выбираем на расстоянии λ от берегов разреза), и проинтегрируем выражение для тока. Тем самым мы установим связь скачков фазы на берегах контура с потоком через контур (в интеграле для вектор-потенциала разрывный контур можно безболезненно дополнить до непрерывного). Особенностью вывода служит то, что точки разрыва контура мы выбираем в точках x и x+Δx, расположенных на малом расстоянии друг от друга.
здесь
Переходя от разности
учитывая, что поток через контур равен
где
Подставив данное выражение для магнитного поля выражение для тока, описывающее эффект Джозефсона, в уравнение Максвелла получим следующее нелинейное дифференциальное уравнение для фазы
здесь мы ввели новый параметр размерности длины Данное уравнение хорошо известно в математике и физике и называется уравнением «синус-Гордон» (sine-Gorgon). Уравнение «синус-Гордон» относится к числу точно интегрируемых методом обратной задачи рассеяния нелинейных уравнений, и у него существуют солитонные и многосолитонные решения (солитон – уединенная волна). В нашем случае солитонное решение описывает джозефсоновский вихрь. Рассмотрим частные решения уравнения для фазы. а) Слабое внешнее поле
для фазы и поля получаем затухающие на масштабе λJ решения.
б) Солитонное решение. Перейдем к безразмерной координате и запишем
откуда
с учетом граничного условия
находим
Это и есть солитон уравнения синус-Гордона. Получили область локализации магнитного поля с циркулирующим вокруг бездиссипативным сверхпроводящим током, представляющую из себя джозефсоновский вихрь. Как и абрикосовский вихрь, джозефсоновский вихрь образован незатухающим циркулирующим током. Однако в отличие от абрикосовского вихря джозефсоновский вихрь не имеет нормальной середины – диэлектрическая туннельная прослойка, в которой расположен центр вихря, вся находится в несверхпроводящем состоянии.
Можно показать, что проникновение дожозефсоновских вихрей в туннельный контакт начинается при магнитном поле, большем критического:
в) Сильное магнитное поле.
При таком поле концентрация вихрей велика, расстояние между ними много меньше джозефсоновской длины, на масштабе которой существенные изменения фазы и магнитного поля в плоскости контакта и, следовательно, магнитное поле можно считать постоянным. г) Узкий контакт При
Интегрируя уравнение для фазы,
получим выражение для джозефсоновского тока:
Найдем полный ток
где полный поток
и критический ток джозефсоновского котнакта:
В результате мы получили, что максимальное значение тока через котакт определяется выражением
Таким образом, аналогично СКВИДу, зависимость максимального значения бездиссипативного тока от магнитного потока имеет (квази)периодический характер. Отличие от СКВИДа связано с тем, что для одиночного перехода поток определяется площадью перехода, а для СКВИДа – площадью петли.
|





 к дифференциалу, находим соотношение, связывающее градиент фазы вдоль контакта и градиент потока
к дифференциалу, находим соотношение, связывающее градиент фазы вдоль контакта и градиент потока

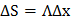
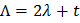 , получим соотношение, выражающее связь производной фазы и значение магнитного поля в данной точке:
, получим соотношение, выражающее связь производной фазы и значение магнитного поля в данной точке:

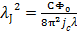 - джозефсоновскую длину. При
- джозефсоновскую длину. При  .
.
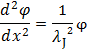
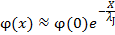
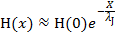


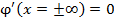
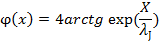

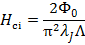
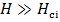
 влиянием поля джозефсоновских токов можно пренебречь и считать магнитное поле в контакте постоянным и равным внешнему магнитному полю:
влиянием поля джозефсоновских токов можно пренебречь и считать магнитное поле в контакте постоянным и равным внешнему магнитному полю: