Вычисление в теории Гинзбурга-Ландау.
Рассмотрим сверхпроводник в сильном магнитном со значением близким к Hc2. Вблизи Hc2 параметр порядка можно считать малым и в 1 уравнении Гинзбурга-Ландау пренебречь кубическим членом. Вернемся к ненормированным величинам. Пренебрегая кубическими членами близи перехода запишем уравнение Гинзбурга-Ландау:
нетрудно заметить, что в таком виде уравнение Гинзбурга-Ландау похоже на уравнение Шредингера для свободного электрона в магнитном поле:
которое, в свою очередь, сводится к уравнению Шредингера для квантового осциллятора с хорошо известным из стандартного курса квантовой механики решением:
Уравнение Гинзбурга-Ландау переходит в уравнение Шредингера для электрона в магнитном поле при следующей замене:
При фиксированном H, чем больше по абсолютной величине параметр
Теперь у нас имеются выражения через параметры функционала Гинзбурга-Ландау как для критического поля Hc, таки для верхнего критического поля Hc2. Из графика зависимости наведенного магнитного момента сверхпроводника от внешнего магнитного поля следует, что
Для отношения критического и верхнего критического магнитного полей имеем:
таким образом существует четкая граница, разделяющая сверхпроводники различного типа:
Выше мы рассматривали формально бесконечный образец, в котором поле зарождение сверхпроводимости при понижении магнитного поля ниже Hc2 происходит в объеме образца. Можно показать, что в сверхпроводнике II рода конечных размеров, помещенном в сильное магнитное поле, зарождение сверхпроводимости происходит вблизи поверхности образца и происходит это при поле Hc3, превышающем поле Hc2. Наличие поверхности требует задания граничного условия при решении дифференциального уравнения Гинзбурга-Ландау и соответствующего ему уравнения для магнитного осциллятора. При этом минимальное значение энергии магнитного осциллятора при фиксированной температуре (фиксированном α) определяет максимальное магнитное поле, при котором возможно существование сверхпроводимости. Таким образом, чем меньше минимальное значение энергии магнитного осциллятора, тем больше критическое значение магнитного поля:
Граничное условие для сверхпроводящего параметра порядка вблизи границы с воздухом имеет вид:
Соответственно магнитное поле. При котором происходит зарождение зародышей сверхпроводящей фазы вблизи поверхности
оказывается выше верхнего критического поля Hc2
|
, тем «сильнее» сверхпроводимость (тем больше амплитуда параметра порядка). Минимальное значение модуля α при котором еще возможно существование сверхпроводимости, т.е. еще возможно существование ненулевого решения линеаризованного уравнения Гинзбурга-Ландау для параметра порядка, соответствует минимальному значению энергии магнитного осциллятора. При фиксированном α сверхпроводимость (ненулевое решение уравнения Гинзбурга-Ландау) может существовать, только если минимальная энергия магнитного осциллятора меньше модуля α. Равенство этих величин определяет верхнее критическое поле Hc2
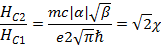
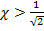- сверхпроводник II-го рода
- сверхпроводник I-го рода
. Решение соответствующего уравнения для магнитного осциллятора можно получить, воспользовавшись аналогом метода изображений в электростатике. Потенциальная энергия осциллятора как функция координаты имеет вид параболы, которая с одной стороны ограничивается поверхностью. Рассмотрим вспомогательную задачу о решении уравнения Шредингера в бесконечной системе с потенциалом, представляющим собой параболу, симметрично отраженную относительно поверхности. Поверхность в такой задаче играет роль плоскости симметрии. В силу симметрии потенциала решение уравнения Шредингера, отвечающее минимальному собственному значению, будет симметрично относительно поверхности, и, следовательно, будет удовлетворять на поверхности условию 
. Ясно, что при такой модификации потенциала его эффективная величина понижается. Поэтому следует ожидать уменьшения минимальной энергии магнитного осциллятора вблизи поверхности. Численный расчет дает для минимальной энергии магнитного осциллятора:
