Семинар 3. Сверхпроводимость и сверхпроводники. История открытия сверхпроводников. Основные виды сверхпроводниковых материалов. Понятие сверхпроводников I и II рода.
Сверхпроводимость относится к числу наиболее фундаментальных физических явлений. Поэтому, чтобы разобраться в принципах работы сверхпроводящих приборов и устройств требуется более детально, чем в стандартном курсе физики твердого тела, ознакомиться с физической сущностью этого явления. Сверхпроводимость было открыто в 1911 г. в Нидерландах, в г. Лейдене в лаборатории под руководством профессора Камерлинга-Оннеса. Главной предпосылкой этого открытия послужило то, что в 1908 г. в этой же лаборатории впервые в мире научились получать жидкий гелий (He) с Тк=4,2К. Лаборатория оставалась монополистом в области получения жидкого гелия до 1923 года, когда эта технология была освоена также Канаде (в СССР – в 1932 г. В Харькове). Впервые сверхпроводимость наблюдалась в ртути (Hg). На рисунке приведен график зависимости сопротивления ртути от температуры. Сопротивление скачком обращается в нуль при температуре равной критической Т=Тс.
Годом позже была открыта сверхпроводимость свинца и олова. Область науки, связанная со сверхпроводимостью довольно быстро развивалась, но прогресс в повышении критической температуры был незначительный:
До 1987г:
В 1987 году произошел качественный скачок, связанный с открытием. высокотемпературной сверхпроводимости (ВТСП). В 1986г. швейцарские физики Беднорц и Мюллер (сотрудники филиала фирмы IBM в г. Цюрихе) обнаружили способность керамики на основе оксидов меди, лантана и бария (La1-xBaxCuO4), при x=0,025 переходить в сверхпроводящее состояние при 34 К. Кроме того, было обнаружено, что с ростом давления Тс увеличивается. Используя этот факт, в феврале 1987 г. профессор университета г. Хьюстона (Техас, США) Чу и др. синтезировали сверхпроводящую керамику из оксидов бария, иттрия и меди YBa2Cu3O7-x с критической температурой 93К, то есть выше точки кипения жидкого азота. Кристаллические структуры этих соединений подобны, но ионный радиус Y меньше, чем La, что приводит к сокращению всех расстояний в структуре, т.е. к эффекту аналогичному действию внешнего давления. Отличительной особенностью большинства известных ВТСП служит наличие плоскостей CuO2. Рекорд на данный момент принадлежит структуре HgBa2Ca2Cu3O8 (Hg-1223), проявляющая сверхпроводящие свойства уже при температуре в 135К. Среди материалов, не содержащих медно-кислородных плоскостей, максимальной температурой (Tc=39K) обладает диборид магния MgB2. В 1933 г. был открыт эффект Мейсснера-Оксенфельда: в объеме сверхпроводника магнитное поле равно нулю
Для понимания свойств сверхпроводников эффект Мейсснера-Оксенфельда даже более важен, чем равенство нулю сопротивления. В первом случае (в магнитном поле) мы имеем дело с термодинамически равновесной системой, в то время, как во втором случае (в электрическом, вызывающем ток) – с неравновесной системой. Из определения магнитной индукции получим:
Для описания сверхпроводника в магнитном поле можно воспользоваться термодинамическими соотношениями и вычислить работу источника магнитного поля, совершаемую при включении магнитного поля Н. В результате находим, что энергия сверхпроводника в магнитном поле выше, чем в отсутствие поля:
FS0 – плотность свободной энергии сверхпроводника в нулевом магнитном поле, FSH - плотность свободной энергии сверхпроводника в ненулевом магнитном поле. При температуре ниже критической в отсутствие магнитного поля энергия сверхпроводящего состояния ниже энергии нормального состояния
При достижении величины магнитного некоторой критической (Hс - критическое магнитное поле) энергии сверхпроводящего и нормального состояний сравниваются.
В точке перехода:
Исходя из этого определения критическое магнитное поле обращается в нуль при температуре равной критической. График зависимости критического магнитного поля от температуры имеет вид:
По своему поведению в магнитном поле все сверхпроводники делятся на две группы: сверхпроводники I и II рода. Сверхпроводник I рода в виде длинного прямого стержня в магнитном поле параллельном оси стержня при достижении полем величины критического поля скачком переходит в нормальное состояние. Данное поведение иллюстрирует следующий рисунок:
В образце сложной формы картина не такая простая. Из-за выталкивания магнитного поля из образца вследствие эффекта Мейсснера вблизи участков поверхности с положительной кривизной происходит сгущение силовых линий магнитного поля.
Вблизи таких участков напряженность магнитного поля может оказаться больше критической при том, что напряженность внешнего поля – меньше критической. В результате магнитное поле проникает в сверхпроводник I рода и он переходит в неоднородное промежуточное состояние, представляющее собой сеть чередующихся областей сверхпроводниковой и нормальной фазы, граница которых всегда параллельна полю. Поле в нормальной фазе всегда равно Для тела, которое можно представить как частный случай эллипсоида вращения (шар, стержень, диск) собственное магнитное поле образца на границе связано с намагничением образца соотношением:
Где n – фактор размагничивания и в сверхпроводниках Для цилиндра, параллельного полю n=0. Для цилиндра, перпендикулярного полю n=1/2. Для шара n=1/3 и на его экваторе имеем:
Таким образом при Поведение в магнитном поле сверхпроводников II рода носит более сложный характер. Как впервые показал А.А.Абрикосов на основе анализа уравнений Гинзбурга-Ландау, при некотором поле Hc1, называемом нижним критическим полем, магнитное поле начинает проникать в сверхпроводящий образец в виде тонких нитей, вокруг оси которых циркулирует сверхпроводящий ток подобно потоку газа или жидкости в вихре.
Структура этих вихрей и их пространственное распределение в виде треугольной решетки носит универсальный характер во всех сверхпроводниках II рода, а сами вихри получили название абрикосовских вихрей. При дальнейшем увеличении магнитного поля концентрация вихрей плавно увеличивается, пока сверхпроводящая фаза не исчезает полностью при верхнем критическом поле Hс2. Различие сверхпроводников I и II рода связано с различными свойствами границы раздела между сверхпроводящей и нормальной фазами в этих сверхпроводниках. В сверхпроводнике I плотность поверхностной энергии σ;>0, а в сверхпроводнике II рода σ;<0. Важную информацию предоставляет температурная зависимость теплоемкости.
С понижением температуры при температуре сверхпроводящего перехода теплоемкость скачком увеличивается, а затем экспоненциально убывает с понижением температуры. Экспоненциальная зависимость от температуры при низких температурах свидетельствует о наличии щели в спектре элементарных возбуждении сверхпроводника. Семинар 4. Термодинамика сверхпроводников. Теорема Нернста. Энтропия сверхпроводящего состояния. Теплоемкость сверхпроводников. Фазовые переходы I и II рода.
Основываясь на известных экспериментальных фактах о поведении сверхпроводника в магнитном поле и температурной зависимости теплоемкости, рассмотрим термодинамику сверхпроводящего состояния. Прежде всего запишем известные соотношения для энтропии и теплоемкости:
Как мы уже показали:
откуда немедленно следует
Данное соотношение позволяет сделать важные выводы: 1. Поскольку экспериментально установлено, что для всех сверхпроводников критическое магнитное поле убывает с ростом температуры и производная критического поля по температуре есть величина отрицательная, то 2. Из III начала термодинамики (теорема Нернста) следует, что при T=0, S=0 => 3. При T=Tс, Hс=0 => Если же переход в сверхпроводящее состояние происходит при понижении температуры в фиксированном поле 0<H<Hс или при понижении магнитного поля при фиксированной температуре T<Tс, то это фазовый переход I-го рода ( Для теплоемкости сверхпроводников имеем следующее выражение:
При Т=Тс, Fn=Fs0, Hс=0 и для скачка теплоемкости (на графике выделен красным цветом) получаем соотношение
Известное как формула Рутгерса.
Семинар 5. Электродинамика сверхпроводников. Теория Лондонов (1-е и 2-е уравнения Лондонов). Эффект Мейсснера. Отличие сверхпроводника от идеального проводника. Промежуточное состояние в сверхпроводниках II-го рода. Понятие критического тока в сверхпроводниках. Первой феноменологической (описывающей макроскопические свойства, но не претендующий на объяснение их микроскопической природы) теориейсверхпроводимости стала двухжидкостная модель братьев Лондонов предложенная ими в 1935 г. В этой модели предполагается, что электронная жидкость в сверхпроводнике при температуре ниже критической состоит из двух компонент – нормальной и сверхпроводящей. Нормальная жидкость подчиняется обычному закону Ома, а сверхпроводящая – протекает по кристаллу без трения и ее движение описывается уравнениями механики для движения во внешнем поле в отсутствие столкновений. Пусть n – полная концентрация частиц, nn - концентрация нормальных частиц, ns- концентрация сверхпроводящих частиц. При Т=Тс ns=0, nn=n, При Т=0 ns= n, nn=0, 1-e уравнение Лондонов (вытекает из II-го закона Ньютона
В стационарном состоянии (
Для кинетической энергии с помощью уравнения Максвелла
Где введен новый коэффициент размерности длины
В результате для полной энергии сверхпроводника получаем следующее выражение:
где Распределение магнитного поля должно удовлетворять условию минимума (равенство нулю вариационной производной): От H перейдем к H +
При выводе мы учли определение вариационной производной
и правила изменения порядка следования векторных производных, следующих из тензорной записи ротора
Из условия равенства нулю вариации энергии при произвольных вариациях магнитного поля следует 2-e уравнение Лондонов
Теперь покажем, что из 2-го уравнения Лондонов вытекает эффект Мейсснера. С помощью известной формулы анализа
и с учетом
откуда Физически, механизм эффекта Мейсснера связан с тем, что вблизи поверхности протекает незатухающий ток (мейcснеровский), который экранирует поле. Ток и поле затухают на расстоянии
Идеальный проводник и сверхпроводник. Как уже упоминалось, нулевое сопротивление и эффект Мейсснера – это два независимых свойства сверхпроводников, которые не сводятся одно к другому, т.е. сверхпроводимость не сводится к идеальной проводимости. Действительно, нетрудно показать, что условия
Если вещество в состоянии с идеальной проводимостью поместить в магнитное поле, то в соответствии с законом Ленца будут возникнут токи, экранирующие это поле. В идеальном проводнике токи не затухают и, на первый взгляд, мы имеем картину, аналогичную эффекту Мейсснера. Однако, если несколько изменить опыт и поместить образец в нормальном состоянии в магнитное поле, а потом, охладив, перевести его в состояние с идеальной проводимостью, то магнитный поток через образец не изменится и токи не наведутся. Более того, если теперь выключить магнитное поле то в силу закона Ленца в идеальном образце наведутся незатухающие токи, которые обеспечат сохранение магнитного потока и магнитного поля в образце, т.е. мы получим картину диаметрально противоположную эффекту Мейсснера – образец, сохраняющий магнитный поток в отсутствие внешнего магнитного поля. Критический ток в сверхпроводниковой проволоке. Достаточно сильное магнитное поле переводит сверхпроводник в нормальное состояние. При этом поле может быть создано как внешним током, так и током, протекающим в самом сверхпроводнике. Рассмотрим сверхпроводящую проволоку радиуса а, через которую протекает ток I.
Интегрируя уравнение Максвелла по площади сечения проволоки
используя теорему Стокса, находим связь полного тока и магнитного поля на поверхности проволоки:
При достижении полем величины критического сверхпроводящая часть проволоки вблизи поверхности переходит в нормальное состояние. Ток, при котором достигается критическое значение магнитного поля на поверхности проволочки называется критическим током.
Полностью перейти в нормальное состояние проволока не может, поскольку в этом случае ток будет распределен равномерно по сечению и напряженность магнитного поля на раcстоянии b (b<a) от оси проволоки, которая определяется током, текущим внутри сечения радиуса b станет меньше критической. Таким образом внешняя часть проволоки находится в нормальном состоянии, а внутренняя часть радиуса R – в промежуточном состоянии.
Величина R определяется из условия, что на границе области напряженность магнитного поля равна критической
Ток, текущий в центральной части проволоки, меньше критического. Оставшаяся часть тока Ic-I1 протекает в приповерхностной нормальной области. Для поддержания этого тока в нормальной области возникает электрическое поле, направленное по оси проволоки. При этом внутренняя часть проволоки находится именно в промежуточном состоянии (ячеистая структура на рисунке) и не может быть целиком сверхпроводящей, поскольку в противном случае источник напряжения, создающий электрическое поле в нормальной области, окажется замкнут через сверхпроводник.
|


 .
.







 .
.


 . Размер и форма сверхпроводящих и нормальных областей определяются размером и формой образца, а также величиной внешнего магнитного поля, т.е носит неуниверсальный характер.
. Размер и форма сверхпроводящих и нормальных областей определяются размером и формой образца, а также величиной внешнего магнитного поля, т.е носит неуниверсальный характер.
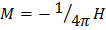 .
.
 - магнитное поле проникает в шарообразный сверхпроводник I и он находится в промежуточном состоянии.
- магнитное поле проникает в шарообразный сверхпроводник I и он находится в промежуточном состоянии.

 ,
, 
 ,
,
 – сверхпроводящее состояние более упорядоченное, чем нормальное
– сверхпроводящее состояние более упорядоченное, чем нормальное
 , следовательно изменение теплоты при таком фазовом переходе не происходит =>
, следовательно изменение теплоты при таком фазовом переходе не происходит =>  - и фазовый переход в сверхпроводящее состояние - фазовый переход II-го рода
- и фазовый переход в сверхпроводящее состояние - фазовый переход II-го рода ).
).
 ,
,
 ,
, ):
): ,
,  ,
,
 ). Следовательно из I уравнения Лондонов получаем, что электрическое поле в сверхпроводнике равно нулю (
). Следовательно из I уравнения Лондонов получаем, что электрическое поле в сверхпроводнике равно нулю ( ). В общем случае (свободная) энергия системы представляет собой сумму кинетической и потенциальной энергий:
). В общем случае (свободная) энергия системы представляет собой сумму кинетической и потенциальной энергий:
 получим следующее выражение:
получим следующее выражение: =
=  ,
,
 .
. – это параметр, определяющий глубину проникновения магнитного поля в материал (см. ниже), и его принято называть лондоновской длиной. Выражение для магнитной энергии имеет обычный вид:
– это параметр, определяющий глубину проникновения магнитного поля в материал (см. ниже), и его принято называть лондоновской длиной. Выражение для магнитной энергии имеет обычный вид: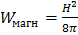 .
. ,
, – это энергия сверхпроводника
– это энергия сверхпроводника  при нулевом магнитном поле (H=0).
при нулевом магнитном поле (H=0).
 , получим
, получим

 ,
,
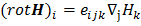


 ,получаем следующее уравнение для распределения магнитного поля в образце
,получаем следующее уравнение для распределения магнитного поля в образце ,
, - магнитное поле затухает в сверхпроводнике на глубине
- магнитное поле затухает в сверхпроводнике на глубине 
 от края образца.
от края образца.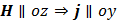 ,
,  .
. недостаточно для того, чтобы магнитное поле в объеме сверхпроводника равнялось нулю
недостаточно для того, чтобы магнитное поле в объеме сверхпроводника равнялось нулю  ,
,
 ,
,

 – критический ток.
– критический ток.





